Учебное пособие: Анализ дифференциальных уравнений
Лекция: Анализ дифференциальных уравнений
Содержание
1. Основные понятия
2. Задачи, приводящие к дифференциальным уравнениям
2.1 Равноускоренное движение
2.2 Геометрические задачи
3. Дифференциальные уравнения первого порядка
3.1 Уравнения с разделяющимися переменными
1. Основные понятия
Дифференциальным уравнением называется уравнение, содержащее независимую переменную х , неизвестную функцию y=y (x) и ее производные y’, y’’,.y ( n) F (x, y, y', y ’’ ,.y (n)) = 0.
Порядком дифференциального уравнения называется наивысший порядок входящей в него производной.
Решением дифференциального уравнения называется всякая функция y=y (x), которая при подстановке в уравнение обращает его в тождество.
Например, уравнение y’’=y’ представляет собой дифференциальное уравнение второго порядка, а функции y (x) = C1 e x + C2 являются его решениями при любых постоянных C1 и C2 .
Процедура поиска решения дифференциального уравнения называется его интегрированием , а графики его решений - интегральными кривыми .
Всякое дифференциальное уравнение порядка n имеет бесчисленное множество решений. Все эти решения определяются функцией, содержащей n произвольных постоянных y =φ (x,C1 ,C2 .Cn ). Эта совокупность решений называется общим решением дифференциального уравнения. Частным решением дифференциального уравнения называется всякая функция этого семейства, отвечающая конкретному набору постоянных C1 ,C2 .Cn .
Геометрически общее решение дифференциального уравнения представляет собой семейство интегральных кривых плоскости XOY , а частное решение - конкретную кривую этого семейства. Например, непосредственным дифференцированием легко проверить, что общим решением дифференциального уравнения y ¢y x =0 является функция y = ![]() . То есть, общее решение уравнения - это семейство окружностей x 2 + y2 = C2 , а
. То есть, общее решение уравнения - это семейство окружностей x 2 + y2 = C2 , а
Начальными условиями для дифференциального уравнения порядка n называется набор значений функции y (x) и ее производных порядка n-1 включительно y ¢ (x), y ¢ (x),.y (n1) (x) в некоторой точке x0 .
Задачей Коши называется задача об отыскании решения дифференциального уравнения F (x, y, y ¢, y ¢,.y (n)) =0, удовлетворяющего заданным начальным условиям:
y ( x0 ) = y0 , y’ ( x0 ) = y1 , y’’ ( x0 ) = y2 ,. y ( n-1) ( x0 ) =yn-1 .
Геометрически это означает, что в общем решении уравнения
y = j (x,C1 ,C2 .Cn ) необходимо так подобрать константы C1 ,C2 .Cn , чтобы соответствующая им интегральная кривая проходила через точку плоскости (x0 , y0 ) и в этой точке имела заданные значения всех своих производных до порядка n-1 . Например, решением задачи Коши y¢y x =0, y (0) =2 является окружность x 2 + y2 = 4 . Чтобы получить это решение необходимо в общее решение уравнения x 2 + y2 = C2 подставить заданные начальные условия x=0 и у=2 и из него найти требуемое значение постоянной C=2.
Приведем без доказательства одну из основополагающих теорем теории ДУ.
Теорема 1. ( существования и единственности решения задачи Коши)
Если функция F (x, y, y ¢, y ¢,.y (n)) непрерывно дифференцируема в некоторой области, содержащей точку (x0 , y0 ), то в этой области существует и притом единственно решение дифференциального уравнения F (x, y, y ¢, y ¢,.y (n)) = 0, удовлетворяющее заданным начальным условиям:
y ( x0 ) = y0 , y’ ( x0 ) = y1 , y’’ ( x0 ) = y2 ,. y ( n-1) ( x0 ) =yn-1 .
2. Задачи, приводящие к дифференциальным уравнениям
2.1 Равноускоренное движение
Пусть в начальный момент времени t=0 материальная точка имеет начальное положение S (0) =0, начальную скорость V (0) = V0 и далее движется прямолинейно с постоянным ускорением a (t) =a . Если S (t) и V (t) - соответственно путь, пройденный точкой за время t , и ее скорость в момент времени t , то, как известно S¢ (t) =V (t) и V ¢ (t) =a (t) =a.
То есть, функция перемещения S (t) является решением дифференциального уравнения S ¢¢ (t) =a . Это решение будем искать, интегрируя уравнение дважды.
V (t) =S ¢ (t) = òS ¢' (t) dt = òadt =at C, V (0) =V0 ÞC =V0 Þ V ( t) = V0 at.
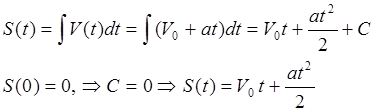
2.2 Геометрические задачи
Пусть, например, требуется найти линию, проходящую через точку А (1,2) и обладающую следующим свойством: для любой ее касательной отрезок этой касательной, заключенный между осями системы координат, в точке касания делится пополам.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--