Учебное пособие: Анализ дифференциальных уравнений

Решение . Сначала найдем общее решение дифференциального уравнения.

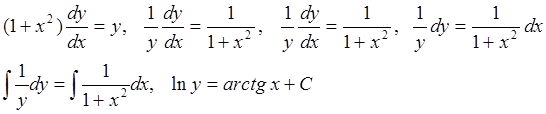
В полученное общее решение подставим заданные начальные условия x=1 и у=1 : 0=ln1=acrtg1+С=π /4+С. Значит, частное решение уравнения, удовлетворяющее заданным начальным условиям, получается из его общего решения при значении постоянной С=-π/4. Решением задачи Коши является функция lny=acrtgx-π/4 , или y = e ^{arctg x - π / 4.}

Однородные уравнения.

Так называются уравнение вида . С помощью замены переменной z (x) =y (x) /x это уравнение может быть сведено к уравнению с разделяющимися переменными. Действительно, тогда

y =x ×z, Þy ¢ = (x ×z) ¢ Þy ¢ =z xz ¢

и для функции z (x) получаем уравнение с разделяющимися переменными

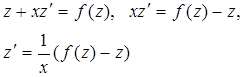
Решив это уравнение, найдем функцию z (x), а с ней и решение исходного уравнения y (x) =x z (x).

Пример 1 . Найти общее решение уравнения

Решение . Разрешим уравнение относительно производной

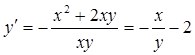
и обозначим . Тогда и для функции z (x) получаем уравнение:

Это уравнение с разделяющимися переменными.

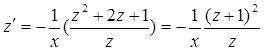
Выразим в нем производную через дифференциалы и разделим переменные

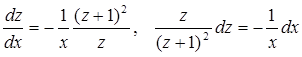
Теперь проинтегрируем обе части последнего уравнения

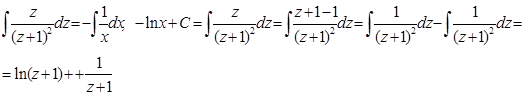
Отсюда

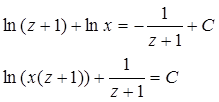
Подставив в последнее равенство z=y/x , найдем общее решение исходного уравнения

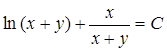
Пример 2 . Решить задачу Коши

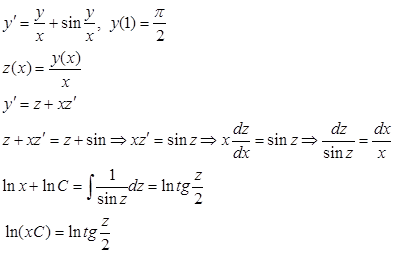
Отсюда z= 2 arctg ( Cx) и, значит, y= 2 x× arctg ( Cx). Подставив в это

равенство начальные условия x=1 и y = π / 2 , получим arctg (C) = π / 4, то есть С=1 . Решением задачи Коши является функция y = 2x × arctgx.

Линейные уравнения.