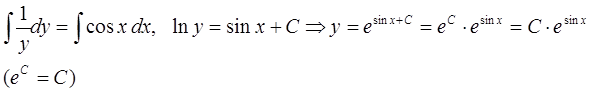Учебное пособие: Анализ дифференциальных уравнений
Касательная к кривой в этой точке имеет уравнение y - y (x0 ) = y' (x0 ) (x - x0 )
Найдем ординаты точек пересечения этой касательной с осями системы координат.
Ясно, что xB = 0 и yC = 0. Тогда:
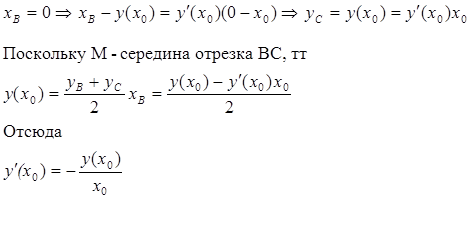
Так как x0 - произвольная точка, то искомая функция должна удовлетворять дифференциальному уравнению первого порядка
![]()
Для произвольной постоянной С функция ![]() удовлетворяет этому уравнению. Поскольку кривая должна проходить через точку А (1,2), то подставив в это решение x=1 и y=2 , получим С=2 . Решением задачи является гипербола
удовлетворяет этому уравнению. Поскольку кривая должна проходить через точку А (1,2), то подставив в это решение x=1 и y=2 , получим С=2 . Решением задачи является гипербола ![]() .
.
3. Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка есть уравнение вида
F (x, y, y ¢) =0.
Далее мы будем полагать, что это уравнение разрешено относительно производной: y ¢ =f (x, y). Это уравнение так же можно записать в дифференциальной форме:
P (x, y) dx + Q (x, y) dy = 0.
Общих методов решения дифференциальных уравнений первого порядка не существует, однако для некоторых важных классов функций f (x,y) такие методы известны и приводят к общему решению уравнения. Рассмотрим некоторые из этих классов.
3.1 Уравнения с разделяющимися переменными
Так называется уравнение, правая часть которого представляет собой произведение функции, зависящей только от х , и функции, зависящей только от у .
![]()
Для поиска решения такого уравнения выразим входящую в него производную через дифференциалы ![]() и перейдем к уравнению в дифференциалах
и перейдем к уравнению в дифференциалах
![]()
Теперь разделим переменные
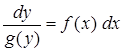
(В последнем уравнении переменные х и у разделяет знак равенства).
Проинтегрировав обе части последнего равенства получаем общее решение уравнения в виде неявно заданной функции:
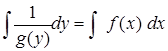
G (y) =F (x) +C .
Рассмотрим практический пример: Найти общее решение уравнения
y' = y cos x.
Решение . Правая часть уравнения представляет собой произведение двух функций, одна из которых зависит от х , а другая от у . Следовательно - это уравнение с разделяющимися переменными. Выразим производную через дифференциалы и разделим переменные:
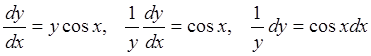
Теперь проинтегрируем обе части последнего уравнения: