Учебное пособие: Анализ дифференциальных уравнений

y ¢p (x) y =q (x).

Решение этого уравнения будем искать в виде произведения двух функций y (x) =u (x) v (x). Тогда y ¢ =u ¢v uv ¢ и относительно функций u и v уравнение примет вид

u ¢v u (v ¢p (x) v) =q (x).

Вместо одной неизвестной функции y (x) мы ввели в рассмотрение две функции u и v , поэтому одной из них мы можем распорядиться по своему усмотрению. Выберем функцию v так, чтобы слагаемое в скобках в левой части последнего уравнения обращалось в ноль. Для этого в качестве v достаточно взять какое-нибудь решение уравнения с разделяющимися переменными

v ¢p (x) v =0 .

Разделяя переменные и интегрируя, получим

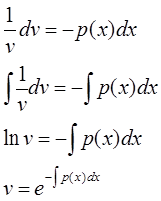
Таким образом, в качестве v достаточно взять функцию

При этом мы можем считать, что константа, возникающая в результате вычисления интеграла, равна нулю. При таком выборе функции v для функции u получаем уравнение

, или

Интегрируя последнее уравнение, получим

Когда функции u и v найдены, общее решение линейного уравнения находится без труда y=uv.

Уравнение Бернулли.

Естественным обобщением линейного дифференциального уравнения первого порядка является уравнение Бернулли

y ¢p (x) y =q (x) y^ .

Метод его решения таков же, как и метод решения линейного уравнения.