Учебное пособие: Анализ временных рядов

Будем считать, что ряд имеет бесконечную предысторию, т. е. время принимает значения t,t-1,t-2,..., - ¥ . Найдем оценку уровня ряда , воспользовавшись минимизацией взвешенной суммы квадратов:

.

В приведенном выражении расхождения между наблюденными значениями ряда и оценкой уровня берутся с экспоненциально убывающими весами в зависимости от возраста данных.

; ; .

Полученную оценку на момент t обозначим (t ). Сглаженное значение в момент t можно выразить через сглаженное значение в прошлый момент t -1 и новое наблюдение :

Полученное соотношение

(t ) =

Перепишем несколько иначе, введя так называемую постоянную сглаживания (0 £a £1).

(t ) ,

Из полученного соотношения видно, что новое сглаженное значение получается из предыдущего коррекцией последнего на долю ошибки, рассогласования, между новым и прогнозным значениями ряда. Происходит своего рода адаптация уровня ряда к новым данным.

4.3.2 Экспоненциальное сглаживание высоких порядков

Обобщим метод экспоненциального сглаживания на случай , когда модель процесса определяется линейной функцией . Как и прежде, при заданном b минимизируем:

.

(Здесь для удобства представления знаки ~ и Ù опущены).

,

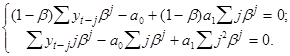
С учетом того что

, ,

получаем

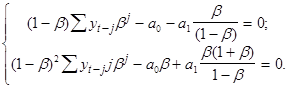
Запишем : .

Эту операцию можно рассматривать как сглаживание 1-го порядка. По аналогии построим сглаживание 2-го порядка:

.

ß