Учебное пособие: Фізика напівпровідників

Коефіцієнт пропорційності називається магнітною сприйнятливістю; це безрозмірна величина, що залежить від природи магнетика.

Величини , , , а також і зв’язані між собою:

; ; ; .

Крива залежності В (Н) називається кривою намагнічування.

Речовини, для яких , , називаються парамагнетиками (; ; ; FeCl).

Речовини, для яких , , називаються діамагнетиками (; ; Zn; ; ; He; Аr; Сr; Ne).

Речовини, для яких , називаються феромагнетиками (Fe; Со; Ni).

Феромагнетики відрізняються від парамагнетиків і діамагнетиків рядом властивостей:

а) крива намагнічування феромагнетика має складний характер (мал. 4.18), тоді як для парамагнетиків вона являє собою пряму з додатнім кутовим коефіцієнтом, а для діамагнетиків – пряму з від’ємним кутовим коефіцієнтом;

б)магнітна проникність феромагнетиків залежить від напруженості поля; у діа- і парамагнетиків – не залежить;

в) розмагнічений феромагнетик намагнічується зовнішнім магнітним полем; залежність В(Н) виражається кривою 01 (мал.4.18). При зменшенні Н до нуля В(Н) змінюється по кривій 1-2; має місце відставання зміни індукції від зміни напруженості. Це явище називається магнітним гістерезисом. Магнітна індукція, що зберігається в феромагнетику після зникнення зовнішнього поля (коли Н=0), називається залишковою магнітною індукцією (Вr). Щоб розмагнітити феромагнетик, треба зняти залишкову індукцію; для цього потрібно створити поле протилежного напрямку. Напруженість поля Нс (відрізок 03 на мал.4.18), при якій магнітна індукція дорівнює нулю, називається коерцитивною силою.

Така залежність В (Н) називається петлею гістерезису.

Властивості феромагнетиків пояснюються наявністю в них областей спонтанної намагніченості – доменів. Розташування магнітних моментів доменів у відсутності зовнішнього поля – хаотичне, тому і сумарна намагніченість дорівнює нулю. В зовнішньому полі магнітні моменти доменів повертаються вздовж поля і феромагнетик намагнічується.

§ 4.11. Вільні електромагнітні коливання

Вільні електромагнітні коливання виникають в ідеальному коливному контурі, що складається з конденсатора ємністю С та котушки індуктивністю L (мал.4.19). Конденсатор заряджається від джерела постійної напруги (ключ К в положенні 1) і в момент часу t=0 під’єднується до котушки (ключ К в положенні 2). Процес розрядки конденсатора супроводжується збільшенням сили струму в котушці; отже, з’являється е.р.с. самоіндукції. Згідно з правилом Лєнца, струм самоіндукції тече проти струму розрядки. Через чверть періода конденсатор повністю розряджений, а сила струму в котушці досягає максимуму. Далі сила струму в котушці зменшується, а струм самоіндукції, згідно з правилом Лєнца, тече в тому ж самому напрямку, що і струм розрядки, перезаряджаючи конденсатор. Далі такі процеси повторюються у зворотньому напрямку, і в момент часу t=Tсистема повертається у вихідний стан.

Періодичні зміни заряду на пластинах конденсатора та сили струму в котушці називаються електромагнітними коливаннями. Якщо втрати енергії на нагрівання відсутні (контур ідеальний, R=0), то коливання будуть незгасаючими. Запишемо для такого контура 2-й закон Кірхгофа: , де – напруга на конденсаторі, –е.р.с. самоіндукції. Підставивши вирази для цих двох величин в 2-й закон Кірхгофа, після нескладних перетворень отримаємо

, (4.48)

де – циклічна частота вільних електромагнітних коливань (власна частота). (4.48) являє собою диференціальне рівняння вільних електромагнітних коливань; його розв’язок має вигляд

(4.49)

(кінетичне рівняння вільних електромагнітних коливань). Період вільних електромагнітних коливань

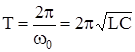(4.50)

(формула Томсона).

Знайдемо тепер вираз для сили струму в котушці контура: , або

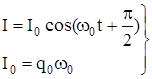(4.51)

Видно, що коливання сили струму І випереджують коливання заряду qна чверть періода (мал. 4.20).

При вільних гар-монічних коливан-нях в коливному контурі відбуває-ться періодичне перетворення енер-гії електричного поля конденсатора 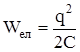в енер-гію магнітного поля котушки: .

Величини та змінюються від 0 до максимальних значень, рівних, відповідно, та . Коливання і Wм зміщені за фазою: в ті моменти часу, коли , і навпаки. Повна енергія електромагнітних коливань в контурі з часом не змінюється:

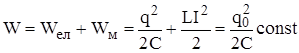. (4.52)

§ 4.12. Згасаючі електромагнітні коливання

Згасання коливань в реальному коливному контурі, опір якого R, обумовлене втратою енергії на нагрівання провідників.

Запишемо для реального контура (мал.4.21) 2-й закон Кірхгофа: