Учебное пособие: Геометрические построения на плоскости

Алгебраический метод решения задач на построение сводится к построению отрезков, заданных формулами.

Полная формулировка задачи: даны отрезки . Пусть а, в, с,…, d – их длина при некоторой единице измерения. Требуется построить с помощью данных инструментов (циркуля и линейки) отрезок , длина которого x(при той же единице измерения) выражается через длины данных отрезков формулой х = f (a, в² , с,…, d). Будем рассматривать такие значения а, в, с,…,d, при которых f имеет смысл и положительна.

Мы уже знаем, как cтроить выражения

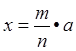, , , , х = а ± в,(а - в, при а >

в). К рассмотренным построениям можно свести построение более сложных формул:

1) , n = натуральное число; делается так:

, причем , если n = p·q,

, если n = p² ± q² ;

2)

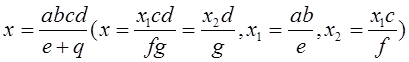
3) · и т.д.

Все построенные выше формулы обладают одним общим cвойcтвом: они являютcя однородными выражениями первой степени. Напоминаем, выражение F(а,…,с) называют однородным степени 11, если

F(ta,…,tc) = tⁿ · F (a,…,c).

Пользуясь понятием однородной функции, мо;но выделить некоторые, классы алгебраичеcких выражений, которые могут быть построены циркулем и линейкой. Например, циркулем и линейкой можно построить:

1) Oтрезок, заданный формулой

,

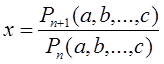где P_{n +1} (…) и P_n (a,b,…,c) - однородные многочлены с рациональными коэффициентами от длин а,в,…,с отрезков степени соответственно n+1 и n.

Пусть

P_{n +1} =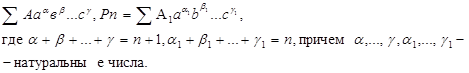

Далее, пусть - произвольный отрезок, d - его длина (в той же единице измерения).

Разделим чиcлитель на dⁿ , знаменатель – на d^{n -1} .

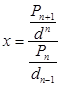
Выражение представляет сумму одночленов вида .

Следовательно, можно построить каждое слагаемое, а потому и весь числитель: 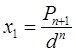. Аналогично, . Наконец строим - отрезок длины х, где ;

2) отрезок, заданный формулой , где – ((…) – однородная рациональная функция 2 степени с рациональными коэффициентами. Делается так: , где (R₂ (…) - отношение двух однородных многочленов , тогда 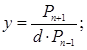как и выше, строим

3) Замечание. При вычерчивании кривых иногда приходится строить алгебраические выражения, не являющиеся однородными первой степени. Пусть надо построить отрезок , длина которого x = f(a,b,…,c), где f(…) не является однородной первой cтепени, например, y = x³ +1.

Правило: построение произвольного выражения от n аргументов всегда можно свести к построению некоторого однородного выражения первой степени от n+1 аргументов. Достигается это выбором единицы измерения.

Выберем некоторый отрезок в качестве единичного, e =1.

-однородная функция первой степени.