Учебное пособие: Геометрические построения на плоскости

Примеры:

1)

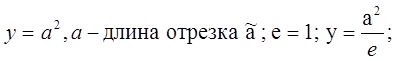
2)

3)

4)

5)

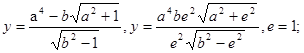
Разрешимость задач на построение с помощью циркуля и линейки.

Для краткости операции «+», «-», «·», «:» и извлечение арифметического квадратного корня» назовем основными действиями.

Теорема. Отрезок, длина которого задается положительной функцией для данных отрезков, может быть построен циркулем и линейкой тогда и только тогда, когда длина искомого отрезка выражается через длины данных отрезков при помощи конечного числа основных действий.

Достаточность. С помощью циркуля и линейки можно построить отрезок , длина которого x равна соответственно:

а+в

а-в

ав (за счет , е = 1)

(- « -)

Так, как по условию длина искомого отрезка выражается через длины данных отрезков с помощью конечного числа основных действий, то остается единственный возможный случай, когда промежуточный отрезок не сможем построить - это построение разности а-в при а < в.

В таких случаях перейдем к положительной разности с помощью тождества а - в = - (в - а).

Теперь можно последовательно выполнить все построения, соответствующие основным операциям, и через конечное число шагов получим искомый отрезок.

Необходимость. Ясно, что построение отрезка равносилъно построению его концов. Так как можно построить, то существует конечная последовательность основных построений, в результате выполнения которых на каком-то m -м шаге будет построен один конец (обозначим его через А ), а на к -ом - другой конец (точку в ). На плоскости построим прямоугольную декартовую систему координат.

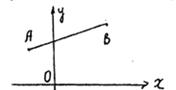
Пусть А (,β), В (γ, δ) - координаты построенных точек. Данные отрезки построим на положительной полуоси ОХ, тогда длины этих отрезков выражаются числами а₁ ,…,а_р ς (А, В) = х = т.е. длина отрезка выражается через числа , β, γ, δ с помощью конечного числа основных действий. Если докажем, что сами числа , β, γ, δ выражаются через а₁ ,…,а_р с помощью конечного числа основных действий, то теорема будет доказана (длина отрезка выражается с помощью конечного числа основных действий).

Заметим, что любые построенные точки в ходе построения появляются двояко: либо выбираемые произвольно, либо как общие точки двух ранее построенных линий.

В первом случае выберем только такие точки, координаты которых выражаются через а₁ ,…,а_р при помощи конечного числа основных действий.

Во втором случае точка получается одним из следующих способов:

а) пересечение прямых (причем каждая прямая проведена через 2 построенные точки):

б) пересечение окружности и прямой (окружность построена через 2 построенные точки);

в) пересечение двух окружностей.

Рассмотрим случай а). Пусть прямая l₁ проведена через точки

C1 (x₁ ,y₁ ) и D₁ (x₂ ,y_2. ). Покажем, что числа х₁ , у₁ , х₂ и у₂ могут быть выражены через а₁ ,…,а_р с помощью конечного числа основных действий (К4ОД). Действительно, пусть уравнение прямой l₁ имеет вид: