Учебное пособие: Характеристика анализа временных рядов

Пример 1 . Рассмотрим динамику валового сбора хлеба и цен на хлеб в России за 1890 –1910 гг., данные представлены в таблице 1.1. Необходимо определить тип модели для аппроксимации имеющихся временных рядов. В качестве критерия оптимальности выбора модели воспользуемся показателем MSD– среднеквадратическим отклонением.

Таблица 1.1

№	Годы	Валовый сбор хлеба	Цены на хлеб	№	Годы	Валовый сбор хлеба	Цены на хлеб
1.	1890	100	100	12.	1901	135	101
2.	1891	78	131	13.	1902	183	102
3.	1892	91	148	14.	1903	174	103
4.	1893	130	114	15.	1904	191	104
5.	1894	139	89	16.	1905	165	108
6.	1895	130	84	17.	1906	143	122
7.	1896	139	85	18.	1907	161	155
8.	1897	122	83	19.	1908	165	168
9.	1898	143	108	20.	1909	204	152
10.	1899	161	109	21.	1910	200	133
11.	1900	152	102

В статистическом пакете Minitabрассматриваются следующие четыре типа моделей: линейная, квадратическая, экспоненциального роста, логистическая S– кривая. Выполним расчеты по каждой из моделей для обоих временных рядов и представим данные расчетов в таблице 2.

Таблица 1.2

Вид модели	MSD
	Валовый сбор хлеба	Цены на хлеб
линейная	296.219	460.058
квадратическая	272.670	258.870
экспоненциального роста	331.586	452.138
логистическая S – кривая	281.557	нет данных

Наиболее точно описывают имеющиеся данные квадратическая модель, так как среднеквадратическое отклонение (MSD) у этой модели наименьшее . Уравнения тренда, описывающие данные временные ряды имеют вид:

– для валового сбора хлеба:

Yt= 84.5263 + 7.88980*t- 0.148474*t2

– для цены на хлеб:

Yt = 130.932 - 7.72938*t + 0.433980*t2

В результате выполнения операции: Stat > Time Series > Trend Analysis и заполнения диалогового окна на экране появятся графики, которые показаны на рисунке 1.2. На графиках видно, что выбранные нами модели тренда достаточно точно описывают имеющиеся временные ряды.

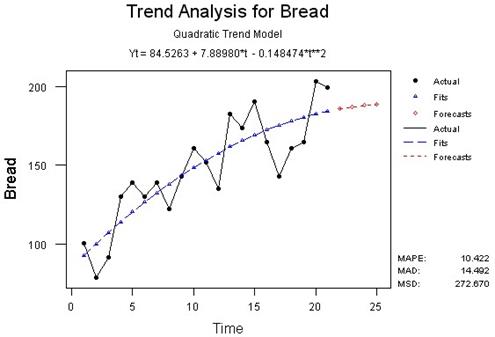
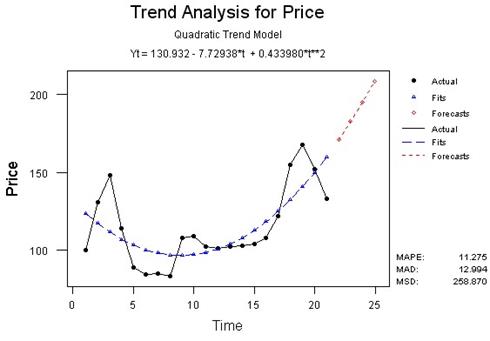
Рисунок 1.2 – Анализ трендов валового сбора хлеба и цены на него

1.2 Декомпозиция временного ряда. Анализ сезонных колебаний

При анализе временного ряда его изменчивость можно разделить на закономерную (детерминированную) и случайную составляющие. Для многих рядов в экономике причины, порождающие их закономерные составляющие не ясны. Тем не менее их совокупное влияние может быть устойчивым в течении достаточно длительных промежутков времени. Это обеспечивает возможность прогноза для подобных временных рядов.

Составная часть временного ряда, остающаяся после выделения из него закономерных (детерминированных) компонент, представляет собой случайную, нерегулярную компоненту. Она является обязательной составной частью любого временного ряда в экономике, так как случайные отклонения неизбежно сопутствуют любому экономическому явлению. Если систематические компоненты временного ряда определены правильно, что как раз и составляет одну из главных целей при разработке моделей временного ряда, то остающаяся после выделения из временного ряда этих компонент так называемая остаточная последовательность (ряд остатков) будет случайной компонентой ряда.

Случайная компонента ряда обладает следующими свойствами:

– случайностью колебаний уровней остаточной последовательности;

– соответствием распределения случайной компоненты нормальному закону распределения;

– равенством математического ожидания случайной компоненты нулю;

– независимостью значений уровней случайной последовательности, то есть отсутствием существенной автокорреляции.

Проверка адекватности моделей временных рядов основана на проверке выполняемости у остаточной последовательности указанных четырех свойств. Если не выполняется хотя бы одно из них, модель признается неадекватной; при выполнении всех четырех свойств модель адекватна. Данная проверка осуществляется с использованием ряда статистических критериев

Закономерную или детерминированную составляющую при анализе экономического временного ряда обычно разбивают на три составляющие : тренд, сезонную компоненту и циклическую компоненту .

Наличие первых двух составляющих временного ряда можно приблизительно определить визуально, построив график временного ряда. На рисунке 1.3 показаны различные виды временных рядов с трендом и сезонной составляющей.

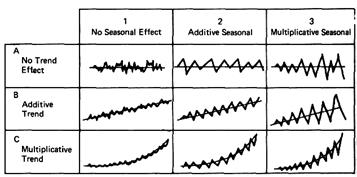
Рисунок 1.3 – Различные виды временных рядов

На рисунке 1.3 введены следующие обозначения:

1 – временной ряд не содержит сезонной составляющей;

2 – временной ряд содержит аддитивную сезонную составляющую;

3 – временной ряд содержит мультипликативную сезонную составляющую;