Учебное пособие: Линейные уравнения и их свойства

Таблица 5

Значения параметров
1	2	2	3	0,5

Решение.

1. Плотность распределения вероятностей является производной функции распределения вероятностей, поэтому:

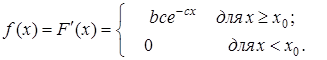
2.Найдем параметр . Функция распределения обладает следующим свойством:=1. Вычислим предел

=.

Отсюда =1.

Далее определим параметр . Интеграл от плотности вероятности по области реализации случайной величины равен единице. В соответствии с условиями задачи спрос как случайная величина изменяется в пределах от до . Поэтому, находя несобственный интеграл, имеем

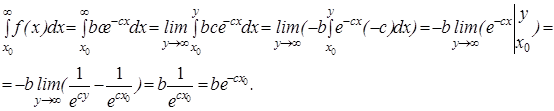
Таким образом, =.

3.Вычислим математическое ожидание спроса через плотность распределения (с учетом того, что =) как несобственный интеграл:

.

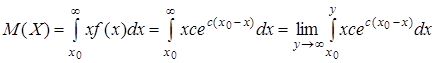Найдем интеграл методом интегрирования по частям. Пусть .

Тогда

.

Применяя формулу интегрирования по частям, получим

.

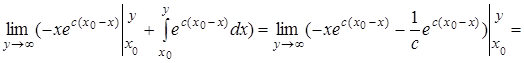
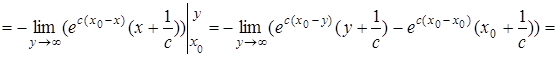
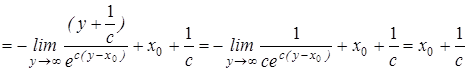Подставив в полученное выражение численные значения параметров, найдем:

По формуле

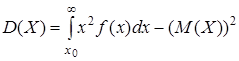
определим дисперсию спроса. Вначале вычислим несобственный интеграл

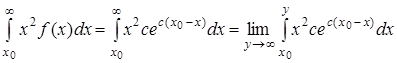
также методом интегрирования по частям. Пусть . Тогда

,

.

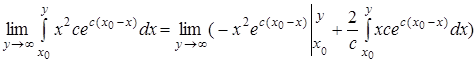Последний интеграл уже найден при вычислении , поэтому можно записать: