Учебное пособие: Линейные уравнения и их свойства

.

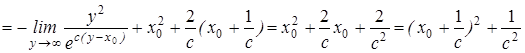Отсюда окончательно получаем:

.

После подстановки численных значений параметров, находим

Среднеквадратическое отклонение вычисляется как квадратный корень из дисперсии:

4. Вероятность нахождения случайной величины в заданном интервале можно найти, используя функцию распределения

При получаем

Подставляя численные значения параметров, имеем:

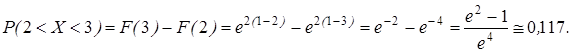
Величина , определяемая равенством , называется квантилем порядка . В задаче требуется найти . Запишем необходимое равенство: или . Логарифмируя последнее равенство , найдем

.

При =0,5 получаем:

Таким образом, с вероятностью 0,5 спрос в случайно выбранном микрорайоне будет больше 1,35 (млн. руб).

Задача для контрольной работы

Функция распределения годовых доходов лиц, облагаемых налогом, описывается выражением:

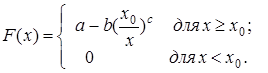
Требуется найти:

1. Плотность распределения вероятности.

2. Параметры и .

3. Математическое ожидание, дисперсию, среднее квадратическое отклонение годового дохода.

4. Вероятность того, что у наудачу выбранного налогоплательщика годовой доход находится в пределах от значения до .

5. Размер годового дохода, который для случайного выбранного налогоплательщика может быть превзойден с вероятностью .

Параметры для различных вариантов заданий приводятся в таблице 6.

Таблица 6

Параметры	Номер варианта
	1	2	3	4	5	6	7	8	9	10
	200	250	300	350	360	370	380	390	400	410
	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0
	210	280	350	400	380	390	410	420	425	440
	230	300	400	480	400	420	430	450	460	500
	0,3	0,35	0,4	0,45	0,5	0,55	0,6	0,55	0,65	0,7