Учебное пособие: Математический анализ. Практикум
4.3.4 Дифференцирование неявной функции
Глава 5. Классические методы оптимизации
5.2 Глобальный экстремум (наибольшее и наименьшее значение функции)
Глава 6. Модель потребительского выбора
6.1 Функция полезности.
6.2 Линии безразличия
6.3 Бюджетное множество
6.4 Теория потребительского спроса
Задания для домашней контрольной работы
Литература
Глава 1. Введение в анализ
1.1 Функции. Общие свойства
Числовая функция определена на множестве D действительных чисел, если каждому значению переменной ![]() поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Аналитическое представление функции:
в явном виде: ![]() ;
;
в неявном виде: ![]() ;
;
в параметрической форме:![]()
разными формулами в области определения ![]() :
:

Свойства.
Четная функция: ![]() . Например, функция
. Например, функция ![]() – четная, т.к.
– четная, т.к. ![]() .
.
Нечетная функция: ![]() . Например, функция
. Например, функция ![]() – нечетная, т.к.
– нечетная, т.к. ![]() .
.
Периодическая функция: ![]() , где T – период функции,
, где T – период функции, ![]() . Например, тригонометрические функции.
. Например, тригонометрические функции.
Монотонная функция. Если для любых ![]() из области определения
из области определения ![]() – функция возрастающая,
– функция возрастающая, ![]() – убывающая. Например,
– убывающая. Например, ![]() – возрастающая, а
– возрастающая, а ![]() – убывающая.
– убывающая.
Ограниченная функция. Если существует такое число M, что ![]() . Например, функции
. Например, функции ![]() и
и ![]() , т.к.
, т.к. ![]() .
.
Пример 1. Найти область определения функций.
![]()
![]()
![]()
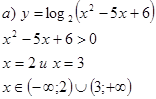 + 2 – 3 +
+ 2 – 3 +
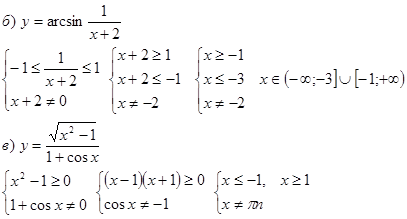
1.2 Теория пределов
Определение 1 . Пределом функции ![]() при
при ![]() называется число b, если для любого
называется число b, если для любого ![]() (
(![]() – сколь угодно малое положительное число) можно найти такое значение аргумента
– сколь угодно малое положительное число) можно найти такое значение аргумента ![]() , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство ![]() .
.
Обозначение: ![]() .
.