Учебное пособие: Методичний матеріал по викладанню алгебри

8

2

5

2. Формулу для обчислення абсолютної величини вектора за його координатами виводжу під час розв’язування вправ (учні по черзі на дошці записують розв’язок):

1) Дано точки А(3;1) і В(5;3). Знайдіть абсолютну величину вектора АВ.

2) Вектор а має початком точку А(x₁ ;y₁ ) ,а кінцем точку B(x₂ ;y₂ ).Знайдіть абсолютну величину вектора а.

Розв’язування.

| a | = | AB | = = .

Пропоную учням обчислити модулі векторів, заданих: а) координатами;

б) початку й кінця (самостійно на кодопозитиві).

3. Для доведення теореми про рівні вектори користуюся мал.13 і розпо відаю сам процес доведення.

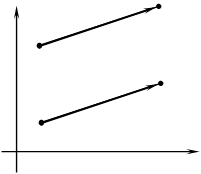y A₂ (x₂ ; y₂ )

A₁ (x₁ ; y₂ )

A₂ '(x₂ ; y₂ )

A₁ '(x₁ '; y₁ ')

O x

Мал. 13

Формулюю пряму і обернену теорему:

” Рівні вектори мають рівні відповідні координати ”.

І навпаки:

”Якщо у векторів відповідні координати рівні, то вектори рівні ”.

На кодоскопу або на таблицях демонструю доведення прямої, і оберненої теореми про рівність векторів. Учні беруть участь в обговоренні доведення.

Пряма теорема: Обернена теорема:

Дано : а = а΄. Дано : x₂ – x₁ = x₂ ΄ – x₁ ΄_, (1)

Довести: x₂ – x₁ = x₂ ΄ – x₁ ΄, y₂ – y₁ = y₂ ΄ – y₁ ΄. (2)

y₂ – y₁ = y₂ ΄ – y₁ ΄. Довести: а = а'.

Доведення. Нехай паралельне пере- Доведення. Знайдеться паралельне, яке перенесення водить точку А₁ в точку А₁ ΄. Тоді , підставляємо

x΄ = x + c, d = y₁ ΄ – y₁ .

y΄ = y + d; І