Учебное пособие: Оптическая физика

Полученные средние значения для каждой пары щелей из группы занести в таблицу 2.

Таблица 2.

Номер пары щелей

d, мкм

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит явление интерференции?

2. Какие волны называются когерентными? Как на практике осуществляются когерентные источники света?

3. Запишите условие усиления и ослабления результирующих колебаний при интерференции?

4. Выведите формулу для ширины интерференционной полосы в опыте Юнга?

5. Как изменяется интерференционная картина в опыте Юнга при изменении расстояния от интерференционного объекта до экрана?

6. Как изменится интерференционная картина в опыте Юнга, если на пути одного из интерферирующих лучей установить плоскопараллельную стеклянную пластинку? Ответ обоснуйте.

ЛИТЕРАТУРА

1. Ландсберг Г.С. Оптика.- М.: Наука, 1976.- 927с.

2. Сивухин Д.В. Общий курс физики. Оптика.- М.: Наука, 1980.- 752с.

3. Годжаев Н.М. Оптика.- М.: Высшая школа, 1977.- 495с.

4. Дитчберн Р. Физическая оптика.- М.: Наука. 1965.- 632с.

Лабораторная работа №2 ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ИНТЕРФЕРЕНЦИОННЫМ МЕТОДОМ

Цель работы: 1) вычислить радиус кривизны выпуклой поверхности линзы; 2) измерить длину световой волны.

Приборы и принадлежности: микроскоп, микрометрическое устройство для измерения диаметра колец Ньютона, плосковыпуклая линза, плоскопараллельная пластинка, ртутная лампа (или электролампа), светофильтры.

Теоретическая часть работы

Общая теория явления интерференции описана в лабораторной работе №6.

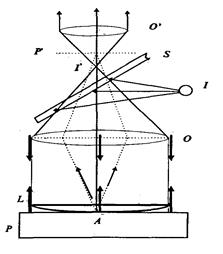
Рисунок 1 – Принципиальная схема наблюдения интерференционной картины колец Ньютона

В данной работе определение длины световой волны осуществляется методом интерференционных колец Ньютона. Схема опыта для получения интерференционной картины в виде колец Ньютона приведена на рис.1. Плосковыпуклая линза L большого радиуса кривизны (1-2 м) накладывается выпуклой стороной на плоскую стеклянную пластинку P. Между соприкасающимися в точке A поверхностями L линзы и пластинки P образуется клинообразный воздушный слой. С помощью наклоненного под углом 45⁰ полупрозрачного зеркала S свет от источника I направляется на объектив O, превращающий падающий на него от зеркала S световой пучок в параллельный, который и освещает линзу L и пластинку P, причем угол падения равен нулю. После отражения от выпуклой поверхности L и соприкасающейся с ней поверхности пластинки P свет проходит в обратном направлении в объектив О, затем в полупрозрачное зеркало S и собирается в точке I’, являющейся изображением точки I. Получившиеся два когерентные световые пучка дают интерференционную картину в виде колец с центром в точке соприкосновения линзы и пластинки P. Т.к. изображение колец Ньютона, даваемое объективом в плоскости P^’ , очень мало, то его рассматривают через окуляр О^’ . В случае освещения белым светом кольца будут окрашены. При освещении монохроматическим светом получаются светлые и темные кольца с убывающей шириной (рис.2).

Рисунок 2 – Схема обозначения правых и левых краев колец Ньютона при измерениях с помощью микрометра.

При отражении от нижней пластинки, представляющей оптически более плотную среду по сравнению с воздухом, волны меняют фазу на противоположную, что эквивалентно изменению пути на l/2. В месте соприкосновения линзы с пластинкой остается тонкая воздушная прослойка, толщина которой значительно меньше длины волны. Поэтому разность хода между лучами, возникающими в этой точке, определяется лишь потерей полуволны при отражении от пластинки, т.е. D=l/2. Следовательно, в центре интерференционной картины наблюдается темное пятно. Т.к. между линзой L и пластинкой P находится воздух (показатель преломления воздуха равен 1) и пучок света падает нормально к пластинке и, практически, к нижней поверхности линзы (кривизна линзы мала), то разность хода в этом случае будет равна D=2h + l/2.

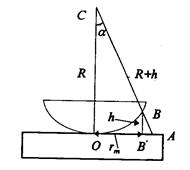
Рисунок 3 – Геометрические построения для вычисления радиусов колец Ньютона.

Для вычисления радиусов колец дополним выпуклую поверхность линзы до полной сферы (рис.3). Если BС - диаметр, то квадрат длины отрезка АО, который мы обозначим через x² , по известной геометрической теореме x² =АО² =(СB + h)² -CO ² . Поскольку СO = CB = R (R - радиус сферы), и, в силу того, что R >> h, выражение для x² можно записать следующим образом: x² =2Rh. Тогда D=x² /R+l/2. Светлые кольца получатся при D=ml, где m - целое число. Из этого условия можно найти радиус r_m m- го светлого кольца:

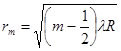. (1)

Аналогично для радиуса m - го темного кольца: