Учебное пособие: Основные понятия и планирование эксперимента

Значения коэффициентов полинома составляют:

.

;

;

;

Если принять, что

,

,

,

то полином имеет вид

.

Значения полинома в точках плана приведены в последнем столбце плана ДФЭ 24-1. В нашем случае точность его достаточно высокая.

Лекция 6. Насыщенные планы первого порядка

Насыщенным планом первого порядка – называется план, содержащий n+1 точку (опыт). Например, при n = 4, N=n + 1 = 5.

То есть полином формируется в виде

.

Таким образом, насыщенный план – это предельно минимальный случай плана ДФЭ. Такие планы называются симплекс-планы. Для симплекс-плана при n = 1 N = 2 его геометрическое изображение представлено на рис. 11, а; при n=2, N=3 – на рис. 11, б; при n=3, N=4 – на рис. 11, в. Симплекс-планы обычно используются на стадии предварительного исследования.

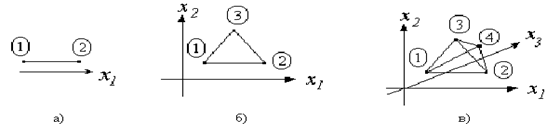
Рис. 11. Симплекс-план для n=1, N=2 (а); n=2, N=3 (б); n=3, N=4 (в)

Симплекс-план не всегда является ортогональным. Симплекс-план называется правильным, если расстояние между двумя любыми точками плана одинаковое. Симплекс-план называется центрированным, если

,

для i=1, 2, …, n .

Применимость планов ПФЭ и пути повышения точности полиномов.

По каким же признакам можно судить о допустимости использования неполного квадратичного полинома, построенного на основе планов ПФЭ 2n?

Такие полиномы дают поверхность отклика, которая проходит точно через все экспериментальные точки, по которым определяются коэффициенты. Так как точки планов ПФЭ располагаются на границах диапазонов варьирования факторов, то это означает, что поверхность отклика проходит через граничные точки. В любом сечении поверхности отклика, полученной по такому полиному, плоскостью при фиксированных всех факторах кроме одного и параллельной оси Y получается след в виде прямой линии.

Возможны случаи, когда реальная поверхность отклика определяется полиномами второго и выше порядков В этом случае поверхность плана ПФЭ, совпадая с реальной поверхностью в граничных точках, может отличаться в других точках факторного пространства, например в центральной точке плана, т.е. . Поэтому одним из признаков неудовлетворительной аппроксимации полиномами по плану ПФЭ является расхождение результатов функции отклика с реальной функцией в центральной точке плана.

Однако при многофакторном эксперименте возможны случаи, когда в реальности функция отклика зависит, в том числе, от квадратов факторов, у которых коэффициенты имеют разные знаки, например, для “седловидной” поверхности. При этом, несмотря на то, что эта поверхность явно нелинейная, результат опыта в центральной точке может оказаться достаточно близким к полученному результату по неполному квадратичному полиному плана ПФЭ. Однако расхождения будут возникать во всех других точках плана эксперимента. Поэтому нецелесообразность использования плана ПФЭ определяется нелинейностью каких-либо сечений поверхности отклика. Косвенным признаком может служить расхождение и в центральной точке плана.