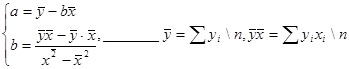Учебное пособие: Особенности эконометрического метода

Парная регрессия- зависимость между 2 переменными Х и У, т.е. модель вида , где у зависимая переменная (результативный признак), х – независимая переменная (факторный признак).

Множественная регрессия – зависимости между 2 и более числом факторов и переменной У, т.е. модель вида: .

Любое эконометрическое исследование начинается со спецификации модели, т.е. формулировки вида модели. При этом парная регрессия достаточная, если имеется доминирующий фактор, который используется в качестве объясняющей переменной Х.

Уравнение парной регрессии характеризует связь между 2 переменными, которая проявляется как некоторая закономерность в целом по совокупности наблюдений. Практически же в каждом отдельном случае величина У складывается из 2 слагаемых , где Уj фактическое значение результативного признака, теоретические значение результативного признака исходя из соответствующей матем. функции, Ej случайная величина, характеризуется отклонением реального значения результативного признака от теоретического, найденного из уравнения регрессии, Е- возмущение и включает в себя влияние неучтенных в модели факторов. Ее присутствие в модели порождено 3 источниками:

1. спецификация модели.

2. выборочный характер исходных данных.

3. особенности измерения переменных.

Основные зависимости, относящиеся к парной регрессии

от правильной спецификации зависит величина случайной ошибки. От тем меньше, чем в большей мере теоретические значения подходят к фактическим данным.

для получения хорошего результата из совокупности обычно исключают единицы с аномальными значениями результативного признака. В парной регрессии выбор вида моделей или математической функции возможен 3 способами:

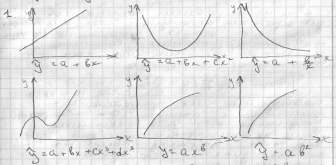
1. графический. 2. аналитический, т.е. исходя из теории изучаемой связи. 3. экспериментальный

при изучении взаимосвязи между 2 переменными графический способ подбора вида уравнений основан на поликорреляции ( исходные данные, обозначенные на плоскости ХОУ).

Основные типы кривых, используемые при количественной оценке связи между 2 переменными.

Аналитический способ типа уравнений основан на изучении материальной природы связи исследуемых признаков.

Например, потребность предприятия в электроэнергии у зависит от объема выполняемой продукции х и всю потребленную энергию можно разделить на 2 части:

1. несвязанную напрямую с производством продукции (а)

2. связанную непосредственно с объемом выпускаемой продукции, которая возрастает пропорционально увеличению объема выпуска (b).

Связь можно изобразить в виде: у=а+bx. При использовании компьютеров для обработки информации выбор вида уравнения осуществляется экспериментальным способом, т.е. путем сравнения величины остаточной дисперсии Дост, которая вычисляется по формуле: где n количество наблюдений исследуемого признака, у- фактические данные, - теоретические данные, полученные по уравнению регрессии. Если уравнение проходит через все точки корреляционного поля, то фактическое значение совпадают с теоретическими. Дост=0.

Практически исследование имеет место некоторая рассеянная точка относительно линии регрессии. Это рассеяние обусловлено влиянием изученных моделей факторов. При экспериментальном способе перебираются разные математические функции в автоматическом режиме и из них выбирается та функция, у которой Дост минимально. Если же Д ост оказывается примерно одинаковой для нескольких функций, то предпочтение отдается более простым функциям.

5. линейная регрессия и корреляция: смысл и оценка параметров

Линейная регрессия сводится к нахождению уравнения вида:

Уравнение вида (1) позволяет по заданным значениям фактора Х найти теоретическое значение результативного признака, представляя в уравнение фактическое значение фактора Х. построение линейной регрессии сводится к оценке этих параметров основан на методе наименьших квадратов (МНК) – позволяет получить также оценки параметров а и b при которых сумма квадратов отклонений теоретических значений результативного признака от фактического значения минимальна, т.е

Это означает, что из всех линий регрессии на графике выбирается так, чтобы сумма квадратов между точками и этой линией по вертикали была минимальна.

Чтобы найти минимум функции нужно вычислить частные производные по каждому из неизвестных параметров a и b и приравнять их к нулю.

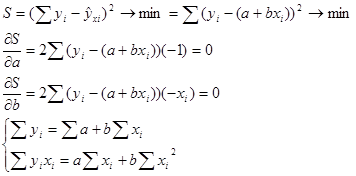
Решение системы будут следующие уравнения.