Учебное пособие: Особенности эконометрического метода

где м –число параметров при переменной х, n –число наблюдений.

Число m характеризует число степеней свободы для факторной суммы квадратов. Величина n-m-1 характеризует число степеней свободы для остаточной суммы квадратов. Для степенной функции для параболы

y=a+bx+cx2 .

9. нелинейная регрессия

Нелинейная регрессия бывает 2 видов:

- регрессии нелинейные, относительно включаемых в анализ объясняющих переменных, но линейные относительно оцениваемых параметров.

- регрессии нелинейные по параметрам.

Примером первого вида являются полиномы различных степеней:

y=a+bx+cx2, y=a+bx+cx2+dx3, y=a+bx+cx2+dx3+…+zxn.’

Сюда же можно отнести равностепенную гиперболу y=a+b/x. Ко второму типу относятся степенная, показательная, экспоненциальная функции. Полиномы любого порядка сводятся к линейной регрессии с ее методами проверки гипотез и оцениванием параметров. Параболу целесообразно применять для оцениваемого интервала значения фактора X, когда меняется характер среди исследуемых признаков. При этом применяется МНК для оценивания неизвестных параметров a,b,c. В результате получается система из 3 линейных уравнений с 3 неизвестными.

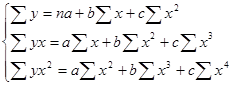
Решение данной системы возможно методом Крамера.

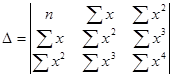
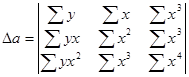
Если b>0, c<0, то кривая симметрична относительно высшей точки, т.е. точки перелома кривой, изменяющей направление связи, а именно рост сменяется падением. Такую функцию используют при изучении зависимости з\п работников от возраста. Если b<0, c>0, то кривая симметрична относительно низшей точки и это позволяет определить минимум в точке, меняющей направление связи, а именно падение сменяется ростом.

Такая функция используется при изучении зависимости объема выпуска производства от затрат на производство. Ввиду симметричности кривой второго порядка ее не всегда удобно использовать в конкретных исследованиях, поэтому если на диаграмме рассеивания нет четко выраженной параболы, то использовать ее не нужно, а заменить степенной функцией. Среди нелинейных функций параметры которой можно найти с помощью МНК y-a+b/x можно назвать равносторонней гиперболой. Примером такой функции является кривая Филипса, которая характеризует соотношение между нормой безработицы Х и приростом з\п У. регрессии нелинейные оцениваемые по параметрам делятся также на 2 вида:

- нелинейные модели внутренне линейные.

- Нелинейные модели внутренне нелинейные.

Если модель внутренне линейна, то она с помощью некоторых преобразований может быть приведена к линейному виду. Если модель внутренне нелинейная, то она не может быть приведена к линейному виду. Внутренне линейной можно назвать y=axb. чтобы привести ее к линейному виду нужно ее линеаризовать с помощью логарифмирования.lny=ln(ax)b; lny=Y, lna=c; blnx=X. Далее в помощью МНК находится коэффициенты С и В c=lna; a=ec. к таким моделям относятся показательная, логистическая функции. В экономических исследованиях степенная функция используется для определения коэффициента эластичности.

.

эконометрика регрессия прогноз ошибка

Коэффициенты эластичности для различных математических функций.

Вид функции У	Первая производная	Коэффициент эластичности
1. линейная y=a+b*x	B
2. парабола 2 порядка y=a+b*x+c*x2	b+2cx
3. гипербола y=a+b\x	-b\x2
4. показательная y=a*bx	a*bx*lnb
5. степенная y=a*xb	a*b*xb-1
6. полулогарифмическая y=a+b*lnx	b/x
7.логистическая y=a\(1+b*e-cx)
8. обратная y=1/(a+bx)	-b\(a+bx)2

Если модель внутренне нелинейная, то для оценки параметров используются итеративные процедуры. Решение такого типа задач реализовано в стандартных пакетах прикладных программ.

10. средняя ошибка аппроксимации

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, тем лучше модель. Величина отклонений фактических данных от теоретических, т.е (y-y^) – ошибка аппроксимации, а т.к. эта величина может быть +\-, то ошибка аппроксимации для каждого наблюдения определяется в % по модулю.

.

Допустимый уровень 8-10%.

11. множественная регрессия и корреляция.спецификация модели

Парная регрессии может дать хороший результат при моделировании, если влиянием др. факторов, воздействующих на объект исследования, можно пренебречь. Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и т.д. основная цель: построить модель с большим числом факторов, определив при этом влияние каждого фактора в отдельности, а также совокупное влияние на моделирование показателей. Множественная регрессия в общем виде можно записать сл. Уравнением:

y=f(x1,x2,…,xn).