Учебное пособие: Переходные и импульсные характеристики электрических цепей

По известной импульсной характеристике цепи можно найти реакцию цепи на заданное воздействие: .

В качестве функции воздействия часто используется единичное импульсное воздействие называемое также дельта-функцией или функцией Дирака.

Дельта-функция – это функция всюду равная нулю, кроме , а площадь ее равна единице ():

.

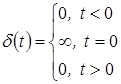К понятию дельта-функция можно прийти, рассматривая предел прямоугольного импульса высотой и длительностью , когда (рис. 3):

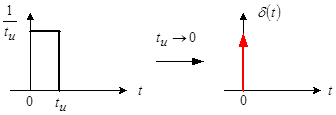
Рис. 3

Установим связь между передаточной функцией цепи и ее импульсной характеристикой, для чего используем операторный метод.

По определению:

.

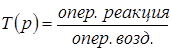Если воздействие (оригинал) рассматривать для наиболее общего случая в виде произведения площади импульса на дельта-функцию, т. е. в виде , то изображение этого воздействия согласно таблицы соответствий имеет вид:

.

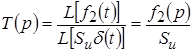Тогда с другой стороны, отношение преобразованной по Лапласу реакции цепи к величине площади импульса воздействия, представляет собой операторную импульсную характеристику цепи:

.

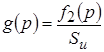Следовательно, .

Для нахождения импульсной характеристики цепи необходимо применить обратное преобразование Лапласа:

, т. е. фактически .

Обобщая формулы, получим связь между операторной передаточной функцией цепи и операторными переходной и импульсной характеристиками цепи:

.

Таким образом, зная одну из характеристик цепи, можно определить любые другие.

Произведем тождественное преобразование равенства, прибавив к средней части .

Тогда будем иметь .

Поскольку представляет собой изображение производной переходной характеристики, то исходное равенство можно переписать в виде:

.

Переходя в область оригиналов, получаем формулу, позволяющую определить импульсную характеристику цепи по известной ее переходной характеристике:

.

Если , то .

Обратное соотношение между указанными характеристиками имеет вид:

.
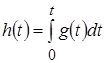