Учебное пособие: Переходные и импульсные характеристики электрических цепей

Эта формула верна для любых значений , поэтому обычно переменную обозначают просто . Тогда:

.

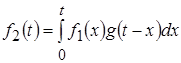Полученное соотношение называют интегралом свертки или интегралом наложения. Функцию , которая находится в результате вычисления интеграла свертки, называют сверткой и .

Можно найти другую форму интеграла свертки, если в полученном выражении для осуществить замену переменных:

.

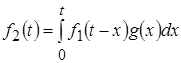Пример: найти напряжение на емкости последовательной -цепи (рис. 8), если на входе действует экспоненциальный импульс вида:

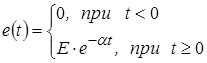
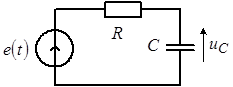
Рис. 8

Воспользуемся интегралом свертки:

.

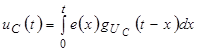Выражение для было получено ранее.

Следовательно, , и .

Тогда

Такой же результат можно получить, применив интеграл Дюамеля.

Литература:

Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. (Учебник)

Бакалов В. П. и др. Теория электрических цепей. – М.: Радио и связь, 1998. (Учебник);

Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974. (Учебник);

Попов В. П. Основы теории цепей – М.: Высшая школа, 2000.(Учебник)