Учебное пособие: Переходные и импульсные характеристики электрических цепей

Если степени числителя и знаменателя одинаковы, то рассматриваемое слагаемое будет присутствовать. Если же функция является правильной дробью, то этого слагаемого не будет.

Пример: определить импульсные характеристики для напряжений и в последовательной -цепи, показанной на рисунке 4.

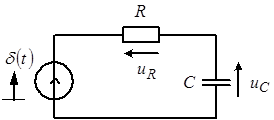
Рис. 4

Определим :

.

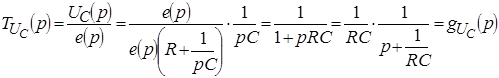По таблице соответствий перейдем к оригиналу:

.

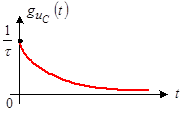
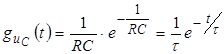График этой функции показан на рисунке 5.

Рис. 5

Передаточная функция :

.

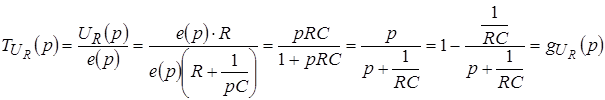Согласно таблице соответствий имеем:

.

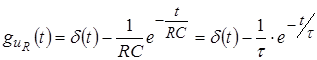График полученной функции показан на рисунке 6.

Рис. 6

Укажем, что такие же выражения можно было получить с помощью соотношений, устанавливающих связь между и .

Импульсная характеристика по физическому смыслу отражает собой процесс свободных колебаний и по этой причине можно утверждать, что в реальных цепях всегда должно выполняться условие:

.

4. Интегралы свертки (наложения)

Рассмотрим порядок определения реакции линейной электрической цепи на сложное воздействие, если известна импульсная характеристика этой цепи . Будем считать, что воздействие представляет собой кусочно-непрерывную функцию , показанную на рисунке 7.

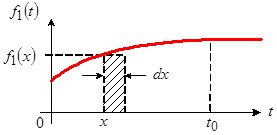
Рис. 7

Пусть требуется найти значение реакции в некоторый момент времени . Решая эту задачу, представим воздействие в виде суммы прямоугольных импульсов бесконечно малой длительности, один из которых, соответствующий моменту времени , показан на рисунке 7. Этот импульс характеризуется длительностью и высотой .

Из ранее рассмотренного материала известно, что реакцию цепи на короткий импульс можно считать равной произведению импульсной характеристики цепи на площадь импульсного воздействия. Следовательно, бесконечно малая составляющая реакции, обусловленная этим импульсным воздействием, в момент времени будет равной:

,

поскольку площадь импульса равна , а от момента его приложения до момента наблюдения проходит время .

Используя принцип наложения, полную реакцию цепи можно определить как сумму бесконечно большого числа бесконечно малых составляющих , вызванных последовательностью бесконечно малых по площади импульсных воздействий, предшествующих моменту времени .

Таким образом: