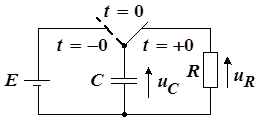Учебное пособие: Переходные и свободные колебания
График данной функции имеет такой же вид, как и на рисунке 4.
Выводы:
1. Временные зависимости всех реакций определяются экспоненциальной функцией.
2. Переходные процессы теоретически длятся бесконечно долго, однако на практике их считают законченными за время ![]() , которое называют временем установления. Изменяя постоянную времени цепи
, которое называют временем установления. Изменяя постоянную времени цепи ![]() можно менять длительность переходного процесса.
можно менять длительность переходного процесса.
3. С физической точки зрения все графики объясняются процессом заряда емкости при ступенчатом воздействии.
Переходные колебания в цепи с индуктивностью
Анализ переходных колебаний в цепи с индуктивностью при воздействии перепада напряжений выполняется аналогично рассмотренному выше. Найдем реакции в последовательной цепи ![]() , показанной на рисунке 8.
, показанной на рисунке 8.


Рис. 8
 ,
,
где ![]() — постоянная времени цепи
— постоянная времени цепи ![]() .
.
Отметим, что при ![]() –
– ![]() , а
, а ![]() , т. е. при перепаде напряжения индуктивность эквивалентна обрыву цепи, а при
, т. е. при перепаде напряжения индуктивность эквивалентна обрыву цепи, а при ![]() эквивалентна КЗ.
эквивалентна КЗ.
Графики временной зависимости напряжений приведены на рисунке 9.
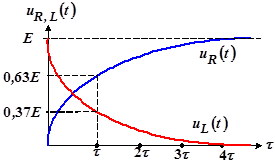
Рис. 9
Изменяя величину ![]() , можно регулировать длительность переходного процесса.
, можно регулировать длительность переходного процесса.
Аналогично можно рассмотреть переходные процессы в параллельной ![]() -цепи при воздействии на нее перепада тока и изобразить графики временной зависимости токов в ветвях
-цепи при воздействии на нее перепада тока и изобразить графики временной зависимости токов в ветвях ![]() ,
, ![]() и напряжения
и напряжения ![]() .
.
Методика нахождения реакций на ступенчатое воздействие в цепях с одним реактивным элементом и несколькими резисторами
Если цепь содержит несколько резисторов, то их по отношению к реактивному элементу известными способами можно свести к одному эквивалентному резистивному сопротивлению. Поэтому ранее полученные выводы справедливы и для этих цепей. В таких случаях для нахождения реакций можно не составлять уравнения в операторной форме, а сразу записать решение в виде:
![]() ,
,
где ![]() и
и ![]() – значения искомой функции соответственно в момент коммутации и в установившемся режиме.
– значения искомой функции соответственно в момент коммутации и в установившемся режиме.
При нахождении величин в приведенной формуле следует пользоваться следующими соображениями:
1. Постоянная времени ![]() находится для
находится для ![]() -цепи
-цепи ![]() для
для ![]() -цепи –
-цепи – 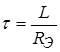 , где
, где ![]() — эквивалентное резистивное сопротивление со стороны зажимов реактивного элемента при погашенном источнике.
— эквивалентное резистивное сопротивление со стороны зажимов реактивного элемента при погашенном источнике.
2. При отыскании ![]() незаряженный конденсатор заменить КЗ, а индуктивность – разрывом.
незаряженный конденсатор заменить КЗ, а индуктивность – разрывом.
3. При определении ![]() конденсатор следует заменить разрывом, а индуктивность – КЗ.
конденсатор следует заменить разрывом, а индуктивность – КЗ.
Свободные колебания в электрической цепи с одним реактивным элементом
4.1. Свободные переходные процессы в цепи с емкостью
Пусть заряженная до напряжения E емкость C в момент времени t = 0 подключается к резистору R (рисунок 10).