Учебное пособие: Переходные и свободные колебания

Рис. 14

За счет энергии, запасенной индуктивностью, происходит процесс свободных колебаний, пока вся энергия не израсходуется на нагрев резистора R . Найдем временные зависимости тока в цепи и напряжений на элементах R и L , которые, как видно из рисунка 14, одинаковы.

На основании 1-го закона коммутации ток через индуктивность не может измениться скачком, т. е. , и в момент времени , , то есть начальные условия ненулевые.

Рассматриваемая схема для момента времени , т. е. сразу же после коммутации, имеет вид, показанный на рисунке 15, при этом индуктивность можно рассматривать как источник задающего тока.

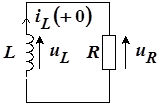
Рис. 15

Для нахождения закона изменения тока в цепи и напряжений на элементах R и L воспользуемся операторным методом, для чего индуктивность с током заменим одной из эквивалентных схем замещения. Здесь удобнее использовать параллельную схему замещения, при этом ток операторного источника тока соответствует начальному току через индуктивность. На рисунке 16 схема замещения индуктивности с током выделена пунктиром.

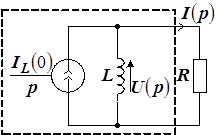
Рис. 16

На основании правила деления токов:

.

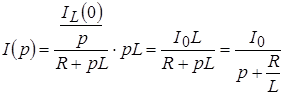Задача в операторной форме решена – получено выражение для преобразованного тока в цепи. На основании таблицы соответствий получим оригинал – временную зависимость тока в режиме свободных колебаний:

,

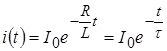где τ = – постоянная времени цепи, имеющая размерность [с].

Так как u_L = u_R , то их временные зависимости также одинаковы. По закону Ома для оригиналов:

.

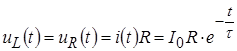Таким образом, в цепи с индуктивностью в режиме свободных колебаний ток и напряжение на элементах R и L будут изменяться (как и в цепи с емкостью) по экспоненциальному закону с постоянной времени τ = . Физический смысл τ такой же, как и в цепи с емкостью. Постоянная времени зависит от параметров цепи R и L и влияет на крутизну экспоненты:

- при увеличении τ , что достигается уменьшением величины R или увеличением величины L , экспонента проходит положе – процесс затухания свободных колебаний замедляется;

- при уменьшении τ , что достигается увеличением величины R или уменьшением L , экспонента проходит круче, и процесс затухания свободных колебаний ускоряется.

При этом , то есть скачок тока невозможен, а , то есть наблюдается скачок напряжения.

Тогда .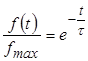

Этот график представляет собой убывающую экспоненту. Крутизна убывания определяется величиной постоянной времени τ . Вид графика не отличается от ранее рассмотренного для цепи с емкостью.

Время окончания свободных колебаний зависит от постоянной времени цепи и определяется так же, как и для цепи с емкостью:

t _УСТ = (34,6)τ .

Примечание: Постоянная времени сложной цепи определяется по формуле, τ = , где R = R _Э – эквивалентное сопротивление, подключенное к элементу индуктивности после совершения коммутации, то есть при . Это сопротивление находится как в обычной резистивной цепи.

В результате анализа свободных колебаний в цепи с одним реактивным элементом можно сделать общие выводы.

1. Реакция (ток, напряжение) цепи на ступенчатое воздействие, формируется путем отключения от цепи источника энергии, представляет собой экспоненциальную убывающую функцию вида:

.

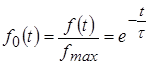Это соответствует физическому смыслу: при отключении источника накопленная энергия убывает, она расходуется на нагрев активного сопротивления.