Учебное пособие: Переходные и свободные колебания

За счет энергии, запасенной в емкости C , в цепи будут происходить свободные колебания. Найдем временные зависимости тока в цепи и напряжений на элементах R и C , которые, как видно из рисунка 10, одинаковы.

Начальные значения тока и напряжения на элементах можно определить на основании законов коммутации. Так как напряжение на емкости не может измениться скачком, то u _C (-0) = u _C (+0) = E , т. е. начальные условия ненулевые. Рассматриваемая схема для момента времени t = +0 (сразу же после коммутации) имеет вид, показанный на рисунке 11, при этом емкость можно рассматривать как источник заданного напряжения.

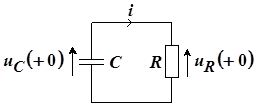
Рис. 11

Применим операторный метод, для чего заряженную емкость заменим одной из эквивалентных схем замещения (иначе нельзя применять закон Ома в операторной форме). В данном случае удобнее использовать последовательную схему замещения. При этом ЭДС операторного источника напряжения соответствует начальному напряжению на емкости. На рисунке 12 схема замещения заряженной емкости выделена пунктиром.

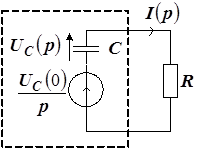
Рис. 12

По закону Ома в операторной форме:

; .

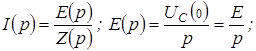
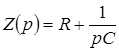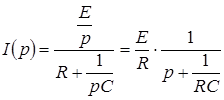Задача в операторной форме решена – получено выражение для преобразованного тока в цепи.

Перейдем от изображения к оригиналу. Согласно таблице соответствий

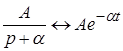. Следовательно: .

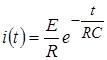Произведение RC обозначается τ , измеряется в секундах и называется постоянной времени RC -цепи.

Так как u _C = u_R , то их временные зависимости также одинаковы. Поэтому, зная выражение для тока в цепи, можно получить и выражение для напряжений на элементах:

.

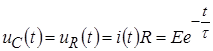Графики полученных выражений целесообразно построить в виде отношения

,

гдеf (t ) = i (t ) илиf (t ) = u _C (t ) = u_R (t ) ,

– максимальное значение определяемой величины, полученное на основании законов коммутации и физического смысла:

(нет скачка),

(скачок напряжения),

(скачок тока).

Заметим, что все эти отношения одинаковы, поэтому достаточно построить один график зависимости 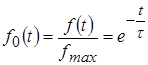. В таблице приведены результаты расчета .

t	0	τ	2τ	3τ	4,6τ	→ ∞
	1	0,368	0,135	0,05	0,01	→ 0

На рисунке 13 показаны графики функций для разных значений τ :

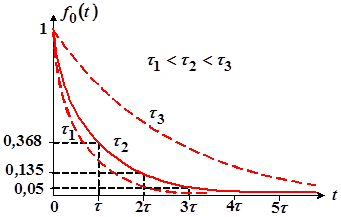
Рис. 13

Данный график представляет собой экспоненту, убывающую с ростом времени t . Важно заметить, что за промежуток времени τ значения экспоненты уменьшаются в е = 2,718… раз, причем такое убывание характерно для любого участка экспоненты.

4.2. Свободные переходные процессы в цепи с индуктивностью

Пусть через индуктивность L протекает ток I ₀ , т. е. при , . В момент времени происходит коммутация – гасится источник (рис. 14).