Учебное пособие: Системы автоматического управления
5. Проверить систему на устойчивость по частотному критерию Михайлова. Сделать выводы.
6. Проверить систему на устойчивость по частотному критерию Найквиста. Сделать выводы.
Ход работы
1. Реализация системы
Передаточные функции звеньев САУ, представленной на рисунке (1), а также разомкнутой и замкнутой систем запишем в общем виде:

На рисунке 2 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения параметров САУ, а на рисунке 3 – представление ее в виде модели в пространстве состояний.

2. Проверка устойчивости системы по критерию Гурвица
На рисунке 4 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения устойчивости системы согласно критерию Гурвица. Очевидно, что исследуемая САУ с заданными параметрами не является устойчивой, поскольку главный определитель системы отрицательный.


3. Определение устойчивости системы по корням характеристического уравнения
На рисунке 5 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения корней характеристического уравнения замкнутой системы. Некоторые корни характеристического уравнения имеют положительные вещественные части, что характеризует систему как неустойчивую.

4. Определение назначения функций ltiview и margin . Получение с их помощью информации о переходной характеристике и запасе устойчивости системы
Функция ltiview запускает так называемый LTIViewer – графический интерфейс пользователя, который упрощает анализ линейных времязависимых систем. Аргументом функции может быть специальная переменная, которая может содержать передаточную функцию системы, либо же описание в любом другом виде, например в пространстве состояний. При помощи LTIViewer можно генерировать временные или частотные графические отклики для изучения ключевых параметров этих откликов, таких как время нарастания сигнала, время регулирования, максимальная амплитуда максимальное перерегулирование и др.
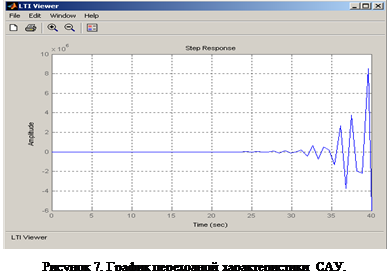
На рисунке 6 представлен фрагмент командного окна MATLAB, на котором изображен процесс запуска интерфейса LTIViewer, а на рисунке 7 – график переходной характеристики системы, по которому однозначно можно судить о неустойчивости последней.

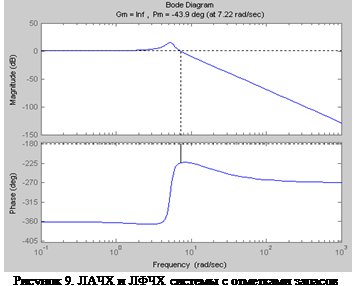
При помощи функции margin можно оценить запас устойчивости системы. Функция выводит диаграмму Боде, на которой отмечает запасы устойчивости по амплитуде и фазе. На рисунке 8 представлен фрагмент командного окна MATLAB, на котором изображен процесс выполнения функции margin , а на рисунке 9 изображена диаграмма Боде для САУ с заданными параметрами с отметками запасов устойчивости по амплитуде и фазе. Как видим, запас по амплитуде равен inf (Gm = inf), а по фазе –43,9º (Pm = -43,9 deg), что свидетельствует о неустойчивости системы.
6. Проверка системы на устойчивость по критерию Михайлова
Для определения устойчивости по Михайлову проведем следующие манипуляции. Характеристический полином замкнутой системы имеет вид:
![]() .
.
Вы полним замену переменных ![]() и получим частотозависимую функцию следующего вида:
и получим частотозависимую функцию следующего вида:
![]() .
.

Вещественная часть этой функции имеет вид: ![]() , а мнимая:
, а мнимая: ![]() .
.
Построим годограф Михайлова при помощи MATLAB, что изображено на рисунке 10. График годографа изображен на рисунке 11.