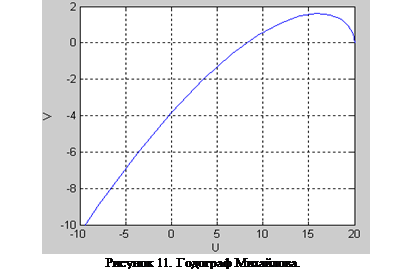
Как видно из рисунка 11, САУ с заданными параметрами неустойчива, поскольку вектор, начало которого лиежит в точке (0, 0), а конец – на кривой Михайлова, вращаясь против часовой стрелки НЕ проходит последовательно количество квадрантов, равное порядку системы – 3.

7. Проверка системы на устойчивость согласно критерию Найквиста

Построение амплитудно-фазовой характеристики (АФЧХ) разомкнутой системы выполняется в командном окне MATLAB при помощи функцииnyquist :

>> nyquist(W)

где W – переменная, несущая информацию о передаточной функции разомкнутой системы.

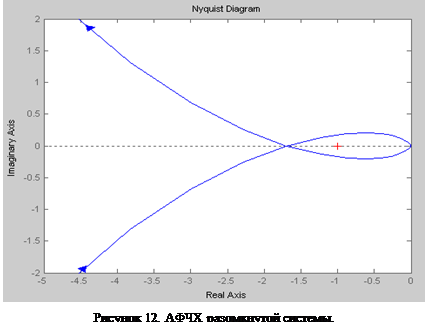
На рисунке 12 построена АФЧЧ разомкнутой системы. Поскольку АФЧХ разомкнутой системы охватывает точку с координатами (-1, j0), то, согласно критерию Найквиста САУ с заданными параметрами является неустойчивой.

Выводы

В работе был проведен анализ устойчивости замкнутой автоматической системы на основании различных критериев при помощи ПО MATLAB.

Эффективность применения ЭВМ и ПО MATLAB в исследовании САУ высокого порядка на устойчивость очевидна, как при применения алгебраических критериев устойчивости, так и графических, поскольку пакет ControlSystem обладает широким набором функций для расчета и отображения характеристик сколь угодно сложной САУ, что было показано в работе.

Лабораторная работа №3. Исследование многоконтурной системы автоматического регулирования

Цель работы

Реализовать и исследовать модель регулирования "жесткого" спутника Земли.

Программа работы

1. Исследовать переходную характеристику объекта регулирования – "жесткого" спутника Земли (ЖСЗ) в среде структурного моделирования Simulink с моментом инерции объекта J = 10 .

2. Охватить динамическую модель "жесткого" спутника обратной связью по положению и оценить устойчивость САУ.

3. Охватить динамическую модель "жесткого" спутника обратной связью по скорости и положению. Системе дана команда изменить угловое положение на 30º. Определить это положение по окончанию переходного процесса. Определить коэффициенты регулятора при следующих коэффициентах демпфирования САР: ξ=0.707, ξ=1.

4. Оценить влияние на переходную характеристику изменения коэффициента обратной связи по скорости.

5. Оценить коэффициенты регулятора, если переходный процесс должен заканчиваться за 0,3 с, при g = 0.

6. Угловая скорость спутника измеряется с помощью гироскопического датчика. Предположим, что датчик вышел из строя (Подобные ситуации действительно имели место). Какой регулятор может обеспечить процесс регулирования САР?

7. Рассмотреть систему с чистым запаздыванием. Оценить динамические свойства системы при различных временах задержки: τ = 0.1 с, τ = 0,4 с, τ = 4 с.

8. Пронаблюдать фазовую траекторию САР.

Ход работы

1. Реализация модели "жесткого" спутника Земли в Simulink

На рисунке 1 представлена структура модели "жесткого" спутника Земли для среды Simulink.

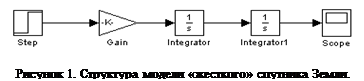
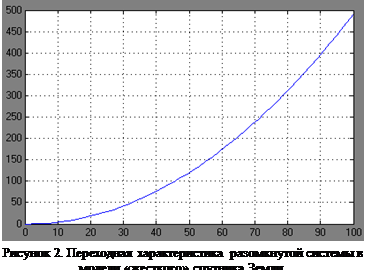
На рисунке 2 изображена переходная характеристика системы, из которой видно, что она не устойчива.

2. Охват модели ЖСЗ обратной связью по положению

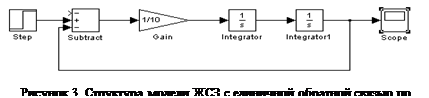
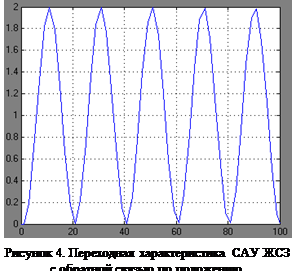
Структура модели ЖСЗ с единичной обратной связью по положению представлена на рисунке 3, ее переходная характеристика – на рисунке 4, вид которой соответствует консервативному звену. Такая САУ находится на границе устойчивости и неспособна привести объект в конечное положение.

3. Охват модели ЖСЗ обратной связью по скорости и по положению