Учебное пособие: Сопротивление материалов

для первого участка:

Q > 0 и М возрастает от нуля до .

Q = const и M  x

для второго участка:

Q < 0 и М убывает с до нуля.

Q = const и M также пропорционален х , т.е. изменяется по линейному закону.

Опасным в данном примере является сечение балки в центре пролета:

Третий характерный пример связан с использованием распределенной по длине балки нагрузки (рис.4). Следуя методике, принятой ранее, очевидно равенство опорных реакций:

,

а для искомого сечения (рис.4, б) выражения для внутренних усилий приобретают вид:

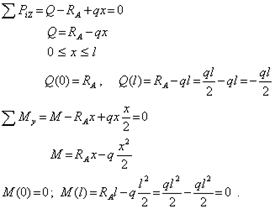
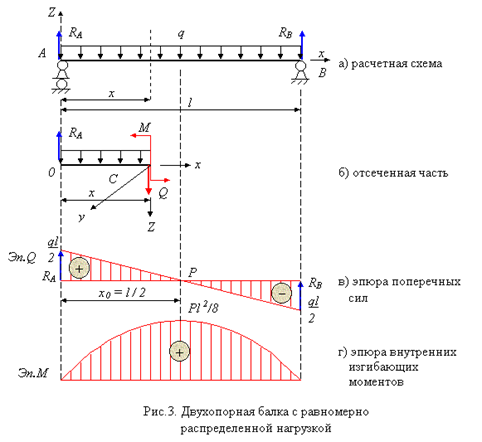
На обеих опорах изгибающий момент отсутствует. Тем не менее опасным сечением балки будет центр пролета при . Действительно, исходя из свойства функции и производной при , внутренний изгибающий момент достигает экстремума. Для нахождения исходной координаты х₀ (рис.3 в) в общем случае приравняем выражение поперечной силы к нулю. В итоге получим

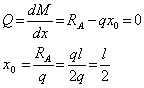
После подстановки в выражение изгибающего момента получим:

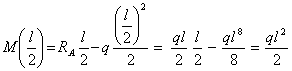
Таким образом,

.

Необходимо отметить, что техника построения эпюр при изгибе наиболее трудно усваивается слушателями. Вам представляется возможность научиться "быстрому" построению эпюр на тесторе-тренажере, приведенном в ПРИЛОЖЕНИИ под грифом Т-4.

5. Понятие о напряжениях и деформациях

Ключевые слова : нормальное и касательное напряжения, линейная и угловая деформации, тензор напряжений.

Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n . В окрестности этой точки выделим малую площадку F . Главный вектор внутренних сил, действующих на этой площадке, обозначим через P (рис. 1, а). При уменьшении размеров площадки соответственно уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при F 0 получим

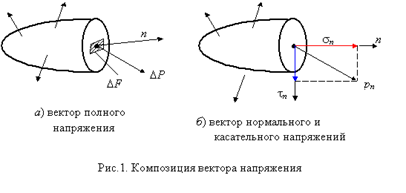
Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор р_n называется вектором напряжений в точке . Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F , характеризуемой вектором n . Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора n определяет напряженное состояние в этой точке.

В общем случае направление вектора напряжений р_n не совпадает с направлением вектора нормали n . Проекция вектора р_n на направление вектора n называется нормальным напряжением s_n , а проекция на плоскость, проходящую через точку М и ортогональную вектору n, - касательным напряжением _n (рис. 1 б).

Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м² .