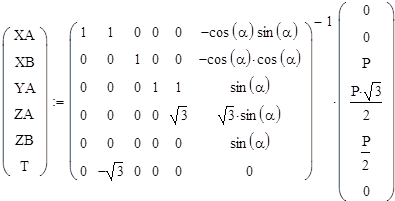Учебное пособие: Теоретическая механика. Статика

Компьютерное решение.

Решаем этуже задачу в в среде Mathcad итерационным методом:

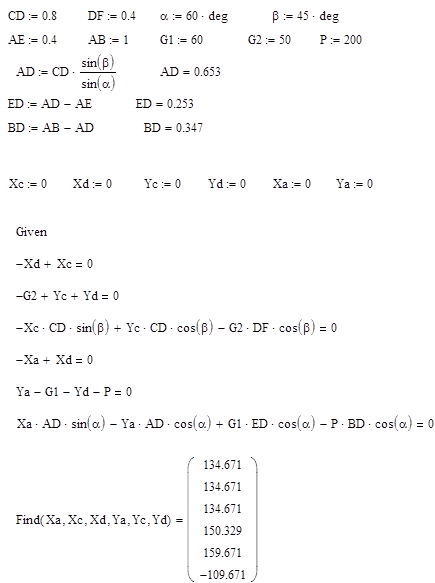
Пример СП-5. Равновесие пространственной системы сил (Мещерский, 8.24)

Однородная прямоугольная рама веса 200 Н прикреплена к стене при помощи шарового шарнира А и петли В и удерживается в горизонтальном положении веревкой СЕ, привязанной в точке С рамы и к гвоздю Е вбитому в стену на одной вертикали с А, причем . Определите натяжение верёвки и опорные реакции.

E x К задаче 8.24.

D

Решение.

Рассмотрим равновесие рамы АВCD и составим расчетную схему сил, действующих на нее (рис. 6).

Как активная сила, действует сила тяжести рамы АВCD , приложенная в центре плиты.

Со стороны связей на стержень действуют их реакции –, и натяжение части веревки ЕС.

Для полученной в расчетной схеме плоской системы сходящихся сил составляем три уравнения равновесия в проекциях на оси координат x, y и z и сумму моментов сил относительно координатных осей x, y и z. () (рис. 6):

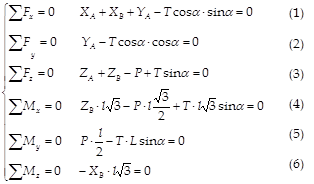
Из уравнения (5) находим . Из уравнение (6) . Из уравнение (4) . Из уравнение (3) находим . Из уравнение (2) . Из уравнение (1)

При заданных числовых значениях получаем T= 200 H, X_A = 86,6 H, Y_A = 150 H, Z_A = 100 H, X_B = Z_B = 0.

Проверка. Для проверки составим еще три уравнения равновесия в форме проекций сил на оси x₁ , y, z₁ (рис. 6) и убедимся, что оно обращается в тождество:

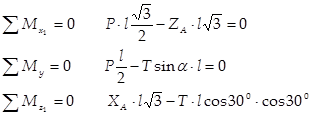
Действительно, при подстановке найденных значений получаем

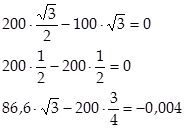
Ответ. Сила натяжения равна Т = 200 Н, опорные реакции X_A = 86.6 Н, Y_A = 150 Н, Z_A = 100 Н, X_B = Y_B = 0.

Компьютерное решение. Для решения системы линейных уравнений можно использовать, например, матричный метод. Уравнения равновесия (1), (2) и (3) запишем в стандартной форме, сохраняя неизвестные в левых частях уравнений:

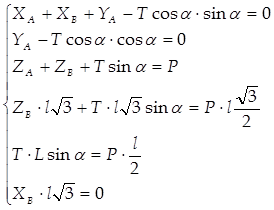
Матричное решение имеет вид: