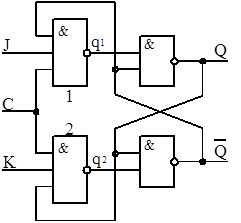Учебное пособие: Типовые логические схемы последовательностного типа

Когда на обоих информационных кодах существуют логические нули (S=R=0), сигналы на выходе могут иметь одно из двух сочетаний: Q=1, =0 либо Q=0, =1, так как каждый логический элемент ИЛИ-НЕ инвертирует входные сигналы, а переключающим сигналом служит единица. Допустим, что Q=1. Этот сигнал, действуя на входе нижнего элемента создаёт на его выходе =0. В свою очередь, на входах верхнего элемента два нулевых сигнала – со входа R и с выхода , обеспечивает Q=1. Состояние это устойчивое.

Если на один из входов подать единичный сигнал, сохраняя нулевой на другом, триггер примет состояние, которое однозначно определяется входной информацией. При входных сигналах S=1, R=0 триггер принимает единичное состояние Q=1, =0, а при S=0, R=1 – нулевое: Q=0, =1. При появлении управляющего сигнала на одном из входов происходит либо опрокидывание триггера, либо подтверждение существующего состояния, если оно совпадает с требуемым.

Если одновременно подать переключающие сигналы на оба входа (S=R=1), на обоих выходах появятся логические нули (Q==0) и устройство утратит свойства триггера. Поэтому комбинацию S=R=1 называют неопределённой (н/о).

Переход от неопределённой комбинации к нейтральной (S=R=0) называют запрещенной комбинацией, так как состояние выходов при этом восстанавливается, но с равной вероятностью оно может стать единичным, так и нулевым, т.е. ведёт к непредсказуемому поведению триггера.

Триггер, который переключается сигналами логической единицы, т.е. на логических элементах ИЛИ-НЕ, называют триггером с прямым управлением (RS-триггер).

Триггер, который переключается сигналами логического нуля, т.е. на логических элементах И-НЕ, называют триггером с инверсными входами (-триггер). Для такого триггера неопределённая комбинация (н/о): S=R=0.

1.2 Триггерные системы

Триггер представляет, как правило, систему, состоящую из триггерной ячейки, играющей роль ячейки памяти (ЯП), и устройство управления (УУ):

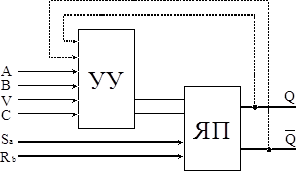
Рис.1.2 Триггерная система:

Q, – внешние выходы;

A, B – информационные (логические) входы;

V – подготовительный вход (предустановка);

С – тактовый вход;

S’, R’ – внутренние входы ячейки памяти;

Sa, Ra – внешние входы ячейки памяти.

Устройство управления – это комбинационное устройство, преобразующее входную информацию в комбинацию сигналов, под воздействием которых триггерная ячейка принимает одно из двух устойчивых состояний.

Изменяя схему устройства управления и способы связи её с триггерной ячейкой, можно получить триггеры с разными функциональными свойствами.

1.3 Асинхронный RS-триггер

У асинхронных триггеров имеются только информационные (логические) входы (т.е. отсутствует устройство управления). Они срабатывают непосредственно за изменением сигналов на входах. Триггерные ячейки на элементах И-НЕ либо ИЛИ-НЕ являются асинхронными RS-триггерами.

1.4 Синхронный RS-триггер

У синхронных триггеров смены сигналов на входах ещё недостаточно для срабатывания. Необходим дополнительный командный импульс, который подаётся на синхронизирующий (тактовый) вход. Это обеспечивается устройством управления, которое связывает каждый из информационных входов с тактовым логической операцией И. Поэтому информация с выводов S и Rможет быть передана на триггерную ячейку только при С=1:

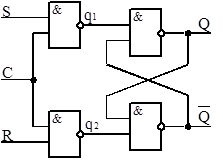
Рис.1.3 Синхронный RS-триггер

Когда С=0, q1=q2=1, что является нейтральной комбинацией для триггерной ячейки, которая хранит записанную информацию, а состояние входов S и R безразлично. С приходом тактового импульса (С=1) триггер изменяет своё состояние или остаётся в прежнем в соответствии с входными сигналами S и R.

Входная комбинация S=R=1 недопустима, так как при С=1 создается недопустимое состояние на выходах Q==1.

Синхронный RS-триггер на элементах ИЛИ-НЕ:

Рис.1.4 Синхронный RS-триггер

Отличие состоит в способе управления: переброс триггера осуществляется сигналами S=0, R=0 при С=0, т.е. нулевыми логическими уровнями.

1.5 JK-триггер

В схемном отношении JK-триггеры отличаются от триггеров RS-типа наличием обратной связи с выходов на входы: