Физика / Учебное пособие: Вихровий характер магнітного поля

Учебное пособие: Вихровий характер магнітного поля

1. Закон повного струму. Використання закону повного струму для розрахунку магнітного поля.

2. Магнітний потік. Теорема Гаусса для магнітного поля.

3. Робота переміщення провідника із струмом і контуру із струмом у магнітному полі.

4. Енергія магнітного поля.

1. Закон повного струму. Використання закону повного струму для розрахунку магнітного поля

Скористаємось рівнянням Максвелла для циркуляції вектора напруженості магнітного поля

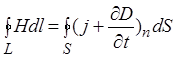, (1.1)

де j – густина струму провідності вільних електричних зарядів; - струм зміщення, не пов’язаний з наявністю вільних електричних зарядів; Н – напруженість магнітного поля.

У провідниках, в яких є вільні електричні заряди, струм зміщення відсутній (він може існувати лише у діелектричному середовищі), тобто

У цьому випадку рівняння (1.1) набуває вигляду:

. (1.2)

Рівняння (1.2) називається законом повного струму. Для написання закону повного струму через індукцію магнітного поля слід замінити Н у формулі (1.2) на

Закон повного струму у цьому випадку матиме вигляд

. (1.3)

Рівняння (1.3) формулюється так:

Циркуляція вектора індукції магнітного поля уздовж довільного замкнутого контуру дорівнює алгебраїчній сумі всіх струмів, охоплених цим контуром і помноженій на ₀ .

Як видно з рівняння (1.3)

Таке магнітне поле називається вихровим. Силові лінії магнітного поля є завжди замкнутими.

Скористаємось законом повного струму (1.3) для розра-хунку магнітного поля соленоїда і тороїда.

а) знайдемо циркуляцію вектора В вздовж замкнутого контуру ABCD (рис.1). У нашому випадку витки в соленоїді щільно прилягають один до одного. Соленоїд має довжину, значно більшу за діаметр.