Учебное пособие: Виконання операцій множення і ділення у двійковій системі числення

Розв'язання . Для даних чисел маємо: =0; = 0, 11100; =0; = 0, 10011. Визначаємо знак добутку: =00=0. Послідовність дій, виконуваних у процесі множення, наведено в табл. 3.5.

Відповідь : С = 0,1000010100.

Метод 4. Якщо перетворити (3.1) за схемою Горнера до вигляду:

,

то множення зведеться до п -кратного виконання циклу:

для початкових значень .

У кожному циклі до суми часткових добутків додається або множене, якщо =1, або нуль, коли =0, після чого сума часткових добутків зсувається на один розряд вліво. Тобто множення починається зі старших розрядiв множника i зсувається сума часткових добутків вліво на один розряд в кожному циклi.

Таблиця 3.5 - Приклад множення з використанням модифікованого пристрою

Для реалізації даного методу множення потрібні (рис.3.5) п -розрядний регістр множеного РгА, п -розрядний регістр множника РгВ з колами для зсуву вліво, п схем І і 2п -розрядний нагромаджувальний суматор НСМ з колами для зсуву вліво. Тут множене завжди додається до п молодших розрядів суми часткових добутків.

Враховуючи те, що в кожному циклі в нагромаджувальному суматорі НСМ спочатку виконується додавання, а потім зсув коду, маємо такий час множення п -розрядних кодів за даним методом:

. (3.5)

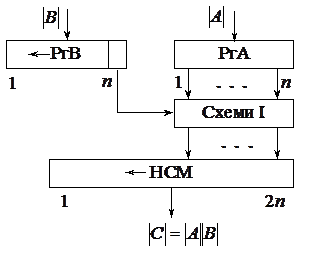
Рис. 3.5. Структурна схема пристрою, що реалізує множення за методом 4

Приклад 3.6. Помножити числа А = 0, 10100 і В = 0, 10011, використовуючи метод 4.

Розв'язання . Для даних чисел маємо: =0; = 0, 10100; =0; = 0, 10011. Визначаємо знак добутку: =00=0. Послідовність дій, виконуваних у процесі множення, наведено у табл. 3.6.

Відповідь : С = 0, 0101111100.

Аналіз описаних методів множення і пристроїв, що їх реалізують показує таке.

Тривалість процесу множення за першим і другим методами менше, ніж за третім і четвертим, за рахунок суміщення у часі операцій додавання часткових добутків і зсувів множеного.

За кількістю апаратури перевагу варто віддати модифікованому пристрою, що реалізує третій метод множення.

Пристрій, що реалізує перший метод множення виявляється дуже не ощадливим за кількістю необхідної апаратури. Крім того, розряди суматора НСМ використовуються неефективно: у початкових циклах множення старші розряди зайняті увесь час "додаванням" нулів, наприкінці множення на молодші розряди надходять з регістра РгА нулі, тобто ніяких корисних операцій вони фактично не роблять.

Таблиця 3.6 - Приклад множення за методом 4

У той же час цей пристрій є вигідним з такої точки зору. До початку множення можна записати в суматор НСМ замість нуля яке-небудь інше число (скажемо, результат попереднього множення). Тоді в результаті множення можна одержати у суматорі НСМ замість добутку значення суми +. Це дозволяє легко організувати нагромадження суми парних добутків чисел . У модифікованому пристрої, що реалізує третій метод, цього зробити не можна, тому що в процесі множення початковий вміст суматора НСМ зсувається п раз управо.

На підставі вищевикладеного можна вважати найбільш зручними для застосування в ЦОМ пристрої, які реалізують перший і третій методи множення, що і підтверджується практикою розробки обчислювальних пристроїв.

3.2.2. Метод скороченого множення

Усі розглянуті методи множення забезпечують одержання добутку розрядністю 2п , не вносячи при цьому похибок у результат. Якщо послідовно буде виконуватись декілька операцій множення, то розрядність результатів буде значно збільшуватись. Тому після виконання операції множення, як правило, здійснюється округлення. Якщо висувається вимога, щоб похибки добутків не перевищували одиниці молодшого розряду (), то можна значно скоротити розрядність регістра множеного РгА і нагромаджувального суматора НСМ. У спеціалізованих машинах іноді реалізують метод скороченого множення, починаючи зі старших розрядів. Особливість цього методу полягає в тому, що одержуються п точних розрядів добутку з використанням розрядів у суматорі НСМ і регістрі РгА.

Кількість додаткових розрядів визначається виходячи з таких міркувань. Нехай і . Тоді, якщо всі , то