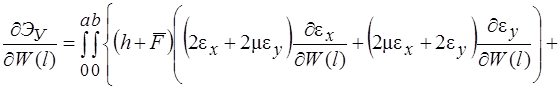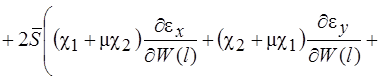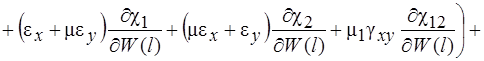Дипломная работа: Алгоритмы параллельных процессов при исследовании устойчивости подкрепленных пологих оболочек

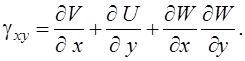
Кроме того, имеют вид (2.7),

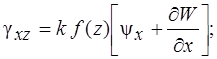
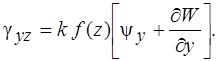
Функции изменения кривизн и кручения принимают вид

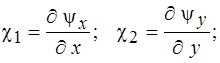
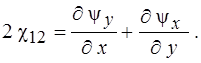(8)

Выражения для здесь принимают вид

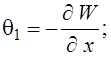
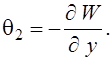(9)

Глава 2. Традиционные алгоритмы решения задач устойчивости для подкрепленных пологих оболочек

После применения метода Ритца к функционалу (1) при аппроксимации функций перемещений в виде

, ,

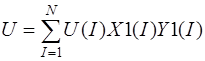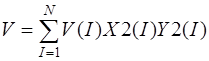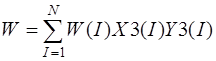, (10)

получим систему интегро-алгебраических уравнений

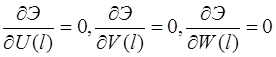(11)

для определения неизвестных числовых параметров , , .

Следует обратить внимание на то, что для конических, сферических и торообразных оболочек аппроксимирующие функции по переменной должны иметь и симметричные, и несимметричные составляющие (если это синусы, то должны быть 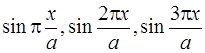и т.д.).

Систему (11) распишем подробно, отдельно вычислив

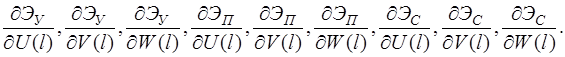
В начале вычислим 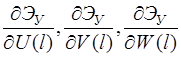, учитывая, что для оболочек вращения 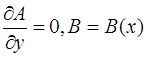, (сомножитель 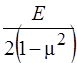опускаем)

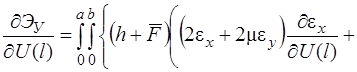
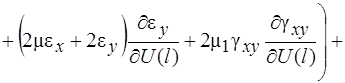
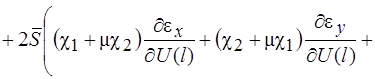
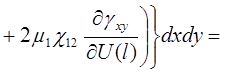
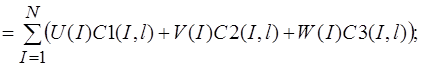(12)

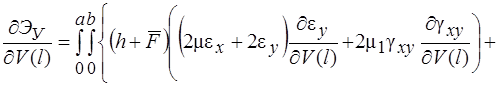
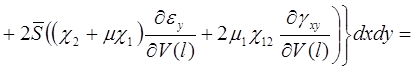
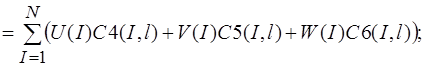(13)