Дипломная работа: Алгоритмы параллельных процессов при исследовании устойчивости подкрепленных пологих оболочек

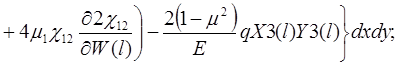
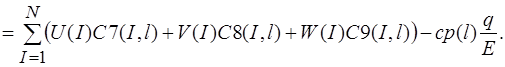(14)

Для решения системы уравнений предполагается использовать метод упругих решений А.А. Ильюшина [9], т.е. метод итераций, когда на каждой итерации решается линейно-упругая задача с изменяющейся правой частью ()

(15)

где равны или . Здесь

, , ,

, , .

В выражениях, стоящих в левой части системы (15), пренебрегается сомножителем 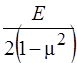, поэтому его не будет и в и .

Так как и будут вычислены при известных , , , то расписывать эти выражения через , , нет смысла. Правые части системы (15) играют роль фиктивной нагрузки.

При вычислении примем

, (16)

где

.

Для металла, не имеющего площадки текучести, принимает значение от до и вычисляется эмпирически, для железобетона

.

Аппроксимация (16) справедлива при малой нелинейности.

Выражение для представим в виде

,

где

(17)

Так как

,

то

(18)

где