Дипломная работа: Алгоритмы параллельных процессов при исследовании устойчивости подкрепленных пологих оболочек
 ,
,  .
.
Теперь вычислим ![]() (опуская сомножитель
(опуская сомножитель
 )
)



 (19)
(19)

 (20)
(20)




 (21)
(21)
Систему (15) кратко можно записать в виде
![]() (22)
(22)
где ![]() равняется
равняется ![]() или
или
![]() ;
; ![]()
![]() - левые части системы (15);
- левые части системы (15);
![]()
![]()
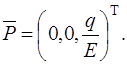
При решении физически-нелинейной задачи для каждого значения параметра нагрузки решается итерационная задача
![]() (23), до тех пор, пока
(23), до тех пор, пока
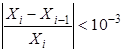 .
.
Начальное приближение ![]() находится из решения линейно-упругой задачи
находится из решения линейно-упругой задачи
![]() (24)
(24)
Метод упругих решений - самый простой и распространенный метод решения нелинейно упругих задач. В работе [15] к уравнениям равновесия применялся метод последовательных нагружений при исследовании напряженно-деформированного состояния плиты в условиях нелинейного деформирования, но для ребристых оболочек такая методика приводит к громоздким уравнениям.
При вычислении 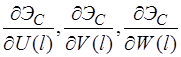 опускаем сомножитель
опускаем сомножитель  . В результате получим два варианта соотношений. Первый вариант получается, если
. В результате получим два варианта соотношений. Первый вариант получается, если ![]() взять в виде (4) и тогда
взять в виде (4) и тогда