Дипломная работа: Формирование понятия функции в курсе математики средней школы

или f(-x) = f(x) (2) для всех хD(f)

Если выполняется равенство (1), то функция у = f(x) четная; если выполняется равенство (2), то функция у = f(x) нечетная. Если не выполняется ни одно из равенств (1) или (2), то функция не является ни четной, ни нечетной.

Можно предложить следующую блок-схему исследования функций на четность и нечетность:

_

+

+

_

+

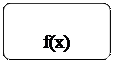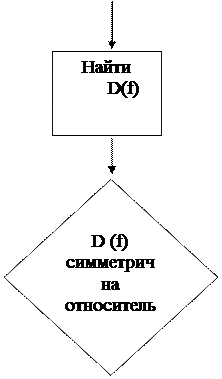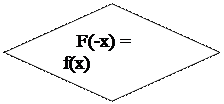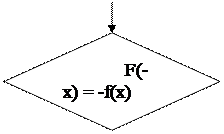Пример : исследовать на четность и нечетность функции:

1) у = 8; 2) у = ; 3) у = ; 4) у = .

Областью определения функции у = 8является числовая прямая (-; +) – симметричное относительно нуля множество. Далее, имеем f(x) = 8;

f(-x) = 8= 8. Таким образом, f(-x) = f(x) , т.е. функция является чётной.

2) Областью определения функции y = является промежуток (0; +) – не симметричное относительно нуля множество, поэтому функция y = не является ни чётной, ни нечётной.

3) Область определения функции у = находится из условия или (x – 1)(x + 1), таким образом, областью определения данной функции является отрезок [-1; 1] – симметричное относительно нуля множество. Далее, имеем

f(x) = ; f(-x) = = , т.е. функция у = является чётной.

4) Функция у = не определена при тех значениях x, при которых знаменатель = 0, т.е. в таких точках –3 и3 значит, область определения функции D(f) = (-; -3) (-3; 3) (3; +) - симметричное относительно нуля множество. Далее f(x) = ; f(x) = = - .

Так как f(-x)f(x) и f(-x)-f(x), то функция не является ни чётной, ни нечётной.

Рассмотрим основные свойства чётных и нечётных функций.

Свойство 1. Если y = f(x) и y = (x) – нечётные функции, то их алгебраическая сумма и разность есть функция нечётная.

Доказательство.

Пусть Функции y = (x) и y = (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму и разность данных функций

(x) и (x) соответственно:

(x) = f(x) + (x); = f(x) - (x).

Так как по определению f(-x) = -f(x) и (-x) = -(x), то

(-x) = f(-x) + (-x) = -f(x) - (x) = - (f(x) + (x)) = -(x)

(-x) = f(-x) - (-x) = -f(x) + (x) = - (f(x) - (x)) = -(x).

Полученные равенства означают, что (x) и (x) – нечётные функции.

Свойство 2. Если y = f(x) и y = (x) – нечётные функции, то их произведение и частное есть функция чётная.