Дипломная работа: Марковская и полумарковская модели открытой сети с тремя узлами

2.1 Дифференциально-разностные уравнения Колмогорова

2.2 Поиск решения дифференциально-разностных уравнений

Колмогорова

2.3 Доказательство инвариантности стационарного распределения

3 МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ И РАЗНОТИПНЫМИ . ЗАЯВКАМИ

3.1 Составление уравнений трафика

3.2 Нахождение решений уравнений трафика

3.3 Уравнения равновесия

3.4 Определение вида стационарного распределения

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Приложение 1 Список опубликованных работ

Приложение 2 Ксерокопии опубликованных работ

ВВЕДЕНИЕ

Теория массового обслуживания предоставляет возможность для адекватного описания и анализа функционирования таких объектов, как телекоммуникационные сети, сети передачи данных, локальные сети, сети ЭВМ, которые получили широкое распространение и развитие в последние годы. В развитие теории сетей массового обслуживания существенный вклад внесли А.А. Боровков, Дж. Джексон, Г.Л. Добрушин, В. А. Ивницкий, Д. Кениг, Ю.В, Малинковский, Г.А. Медведев, А.Л. Толмачев и многие другие.

Отправной точкой в исследовании сетей является нахождение стационарного распределения вероятностей состояний. Поскольку большую часть времени изучаемый объект проводит в установившемся, стационарном режиме. Поэтому исследования по теории сетей, которые функционируют в стационарном режиме, важны как для теории, так и для практики. С помощью стационарного распределения могут быть найдены разнообразные показатели качества функционирования реальных систем: производительность, времена выполнения заданий, загрузка и простои приборов и т.д.

Многие исследования проводились в предположении экспоненциальности времен обслуживания, хотя на практике распределение длительностей обслуживания зачастую отличается от показательного. Поэтому весьма актуальным представляется доказательство инвариантности стационарного распределения состояний сетей относительно функционального вида законов распределений времен обслуживания.

Основной целью работы является исследование стационарного распределения сетей массового обслуживания и доказательство инвариантности.

1. МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ

Определение 1.1. Сетью массового обслуживания называется совокупность одновременно и взаимосвязано функционирующих систем массового обслуживания, в которой циркулируют заявки, переходящие из одной системы массового обслуживания в другую.

Определение 1.2. Системы массового обслуживания, из которых состоит сеть, называют узлами (полюсами, обслуживающими центрами).

Определение 1.3. Сеть называется марковской, если она описывается марковским процессом.

Пусть имеется открытая сеть массового обслуживания, состоящая из трёх узлов, в которую поступает простейший поток заявок с параметром . Причём, в первую систему массового обслуживания, входящая заявка поступает с вероятностью . Времена обслуживания заявок в различных узлах независимы, не зависят от процесса поступления заявок и имеют показательное распределение с параметрами для -ого узла, где - число заявок в -ой системе, .

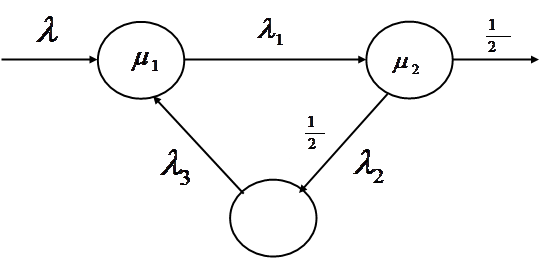
Дисциплины обслуживания заявок в системах сети FCFS. Заявка, завершающая обслуживание в -ом узле мгновенно с вероятностью переходит в -ый узел или с вероятностью покидает сеть, причём . Схематически сеть изображена на рисунке 1.1.

??????? 1.1

Матрица перехода имеет следующий вид:

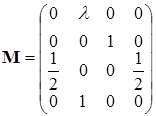
Состояние сети описывается случайным процессом

,

где - число заявок в -ом узле в момент . Покажем, что - марковский процесс. Состояние для определяется:

1) числом заявок в узлах в момент ;

2) моментами поступлений заявок в каждый узел после момента ;