Дипломная работа: Марковская и полумарковская модели открытой сети с тремя узлами

Лемма 1.1 (об “отсутствии памяти” у показательного распределения) .

Если имеет показательное распределение с параметром , то при любых и

.

Доказательство. По определению условной вероятности

.

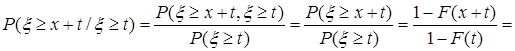
Моменты внешних поступлений в первый узел после момента не зависят от предыстории сети до момента , так как поток извне на первый узел пуассоновский; моменты поступлений заявок с узлов на данный узел после момента в силу “отсутствия памяти” у показательного распределения времени обслуживания заявок в узлах (см. лемму 1.1) . Аналогично доказывается, что моменты уходов заявок из узлов после момента не зависят от предыстории до момента . Таким образом, закон распределения для определяется распределением . Значит, - марковский процесс. [1]

Таким образом, в соответствии с определением 1.3 и вышесказанном, построена марковская модель открытой сети с тремя узлами.

1.1 Уравнения глобального равновесия

Предположим, что существует стационарное распределение. Составим уравнение равновесия для стационарных вероятностей , которые для сетей называются глобальными уравнениями равновесия (баланса ).

Из состояния сеть может выйти либо за счёт поступления заявки в неё (интенсивность ), либо за счёт обслуживания заявки одним из узлов, например, - ым (интенсивность ). Поэтому интенсивность выхода из состояния для марковского процесса равна , где 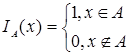- индикаторная функция множества . Следовательно, поток вероятности из состояния равен:

. (1.1.1)

Войти же в состояние можно либо из состояния , если в сеть поступит заявка, направленная в первый узел ( интенсивность ), либо из состояния , если заявка завершит обслуживание во втором узле и уйдёт из сети ( интенсивность ), либо, наконец, из состояний , (,), если заявка завершит обслуживание на первом, (втором, третьем) узле и перейдёт соответственно во второй, ( третий, первый) (интенсивность , (, )). Поэтому поток вероятности в состояние

. (1.1.2)

Приравнивая потоки вероятности из состояния (формула 1.1.1) и в состояние (формула 1.1.2), получаем глобальные уравнения равновесия

. (1.1.3)

1.2 Отыскание стационарных вероятностей

Составим уравнение трафика, используя следующую формулу

, (1.2.1)

,

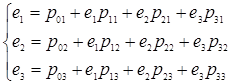где - вероятности перехода.

Решим полученную систему уравнений

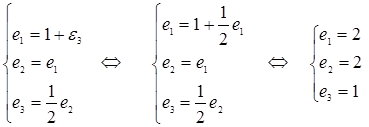
Таким образом, уравнение трафика имеет единственное положительное решение , то есть . Положительное в том смысле, что .

Рассмотрим изолированный -й узел, считая, что на него поступает простейший поток заявок интенсивности (см. рисунок 1.2.1).