Дипломная работа: Марковская и полумарковская модели открытой сети с тремя узлами

Переносим в левую часть равенства, затем делим обе части на и устремляем , получим

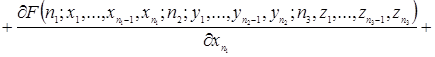
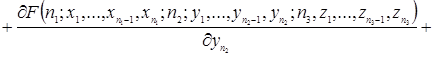
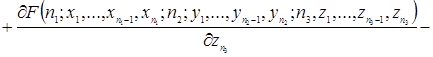
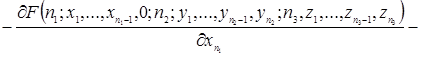
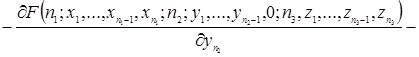(2.1.4)

.

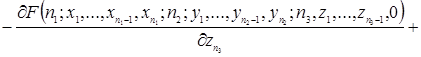
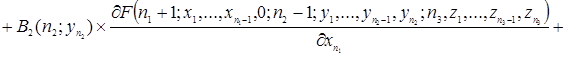
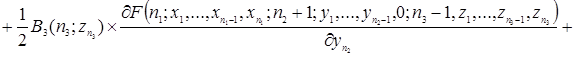
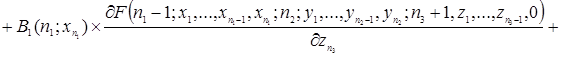
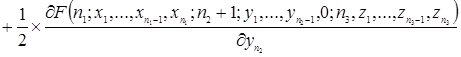Таким образом, уравнения (2.1.4) и есть искомые уравнения Колмогорова.

2.2 Поиск решения дифференциально-разностных уравнений Колмогорова

Решением уравнений Колмогорова (2.1.4) является:

(2.2.1)

.

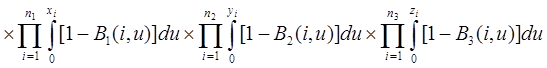Проверим найденное решение (2.2.1) непосредственной подстановкой в уравнения (2.1.4), получим
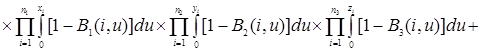
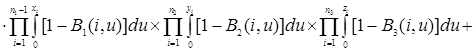
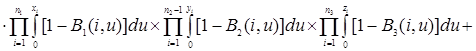
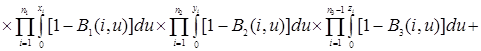