Дипломная работа: Марковская и полумарковская модели открытой сети с тремя узлами
(1.2.9)
=
.
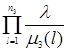1.3 Достаточное условие эргодичности
Теорема 1.3.1 (Эргодическая теорема Фостера).
Регулярная Марковская цепь с непрерывным временем и счетным числом состояний эргодична, если она неприводима и система уравнений
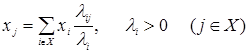
имеет нетривиальное решение 
такое, что 
При этом существует единственное стационарное распределение, которое совпадает с эргодическим. [2, с. 8-14]
Эргодичность исследуем в соответствии с теоремой 1.3.1. Рассмотрим условия теоремы.
Регулярность следует из того, что 
.
, 
, 
.
Согласно рисунку 1.1, получим:
, 
, .
Таким образом, регулярность выполняется.
Так как все состояния сообщаются с нулевым, то есть в любое состояние 
можно перейти из нулевого 
и в можно перейти из любого состояния,путем поступления, обслуживания и ухода заявок из сети, то отсюда следует неприводимость.
Примечание – здесь учитывается, что матрица переходов 
неприводима.
В качестве нетривиального решения системы уравнений из теоремы 1.3.1 возьмем 
. Тогда для эргодичности потребуется, чтобы 
. Тогда получим,
,
где
,
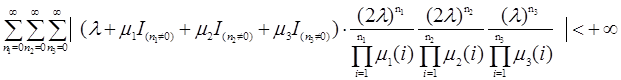
Последний ряд сходится по признаку сравнения, если сходится ряд
|
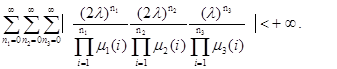
Условие (1.3.1) и есть искомое условие эргодичности. Если это условие будет выполнятся, то будет существовать единственное стационарное распределение, совпадающее с эргодическим.
2. ПОЛУМАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ
Пусть имеется открытая сеть массового обслуживания, состоящая из трёх узлов, в которую поступает простейший поток заявок с параметром 
. Причём, в первую систему массового обслуживания, входящая заявка поступает с вероятностью 
. Времена обслуживания заявок в 
-ом узле заданы функцией распределения времени обслуживания -ым прибором одной заявки 
, 
. При этом налагается следующее требование
, . (2.1)
Дисциплины обслуживания заявок в системах сети LCFSPR - заявка, поступающая в -ый узел, вытесняет заявку с прибора и начинает обслуживаться. Вытесненная с прибора заявка становится в начало очереди. Схематически сеть изображена на рисунке 2.1.
 |
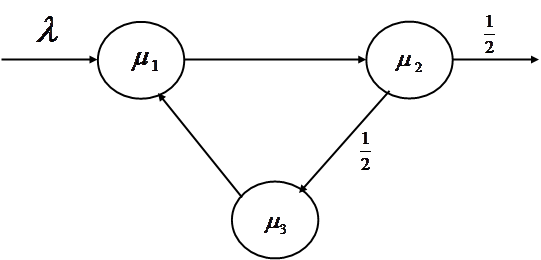Рисунок 2.1
Состояние сети описывается случайным процессом
,
где 
, 
, 
- остаточное время обслуживания заявки, стоящей в -ой позиции.
Примечание. Случайный процесс