Дипломная работа: Математические основы системы остаточных классов

откуда получается следующая индуктивная процедура вычисления и

:

Пример . Применим расширенный алгоритм Евклида к числам а = 342, b = 612. Весь алгоритм представим в виде следующей таблицы.

Расширенный алгоритм Евклида

Номер итерации	q	A 0	a 1	x 0	x 1	Y 0	y 1
0	-	342	612	1	0	0	1
1	0	612	342	0	1	1	0
2	1	342	270	1	-1	0	1
3	1	270	72	-1	2	1	-1
4	3	72	54	2	-7	-1	4
5	1	54	18	-7	9	4	-5
6	3	18	0	9	-34	-5	19

Заметим, что равенство выполняется на каждом шаге итерации. Алгоритм выдаёт d = 18, x = 9, y = -5 и тогда 18=342∙9 + 612∙(-5).

§ 3. Китайская теорема об остатках и её роль в представлении чисел в СОК

Фундаментальным положением, лежащим в основе модулярного представления чисел, является китайская теорема об остатках. Эта теорема формулируется следующим образом.

Теорема . Пусть - попарно взаимно-простые числа, больше 1, и пусть . Тогда существует единственное неотрицательное решение по модулю Р следующей системы сравнений:

…, (3.1)

Другими словами, отображение, которое каждому целому числу х , , ставит в соответствие кортеж , где , , является биекцией кольца на декартово произведение

колец .

Существует много различных доказательств этой теоремы. Приведём конструктивное доказательство китайской теоремы об остатках.

Доказательство. Найдём число х , , удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа х вида где q ₁ – произвольное целое число. Для нахождения q ₁ подставим значение х во второе сравнение системы, после чего получим откуда где - обратный мультипликативный элемент к по модулю . Такой элемент существует, так как Найденное таким образом q ₁ можно записать в виде

для некоторого целого числа . Подставив значение в выражение

Теперь первые два сравнения могут быть заменены на одно

(3.2)

Применим теперь описанную процедуру к сравнению (3.2) и к одному из оставшихся сравнений системы (3.1). Повторяя этот процесс k – 1 раз, мы в конечном итоге найдём число х , удовлетворяющее всем сравнениям системы (3.1).

Докажем единственность решения системы (3.1). Воспользуемся методом от противного. Предположим, что существует другое решение системы (3.1). Тогда

для всех . Вычитая почленно из первого сравнения второе, получим истинное сравнение откуда следует, что . Но тогда , следовательно, , так как . Этим завершается доказательство китайской теоремы об остатках.

Пример . Решим систему сравнений

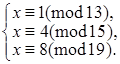
Решение . Так как модули 13, 15, 19 попарно взаимно простые числа, то данная система имеет единственное решение по модулю . Сравнение соответствует диофантовому уравнению , где . Заменяя х во втором сравнении системы на , получаем , т. е. . К числу 13 обратным мультипликативным элементом по модулю 15 является число 7. Умножая последнее сравнение на 7 и, переходя в нём к вычетам по модулю 15, получим . Таким образом, . Следовательно, , при этом все числа вида являются решениями первых двух сравнений данной системы. Подставим в третье сравнение вместо х полученное выше значение или . Так как (5, 19) = 1, то или . Итак,

, то есть х = 274.