3) рассмотрим точки ,, и докажем следующее неравенство:

Возведем это неравенство в квадрат:

.

Так как и (поскольку ) и выражение есть величина неотрицательная, то неравенство является верным.

2. 1)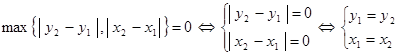

2) так как и , то вторая аксиома очевидна: .

3) рассмотрим точки ,, и докажем следующее неравенство: .

Тогда и .

3. 1)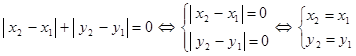

2) так как и , то вторая аксиома очевидна:

.

3) рассмотрим точки ,,.

Неравенство: - очевидно.

· Введенные метрики и эквивалентны, то есть задают одну и ту же топологию.

Пусть метрика порождает топологию , - топологию и - топологию . Достаточно показать два равенства.

Покажем, что .

Рассмотрим множество, открытое в и покажем, что открыто в . Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в . Шар в - квадрат, шар в - круг. А квадрат всегда можно заключить в круг. Тогда открыто и в .

Аналогично доказывается, что . А тогда и .

Глава II. Свойства метризуемых пространств

Свойство 1. Метризуемое пространство хаусдорфово.

Доказательство. Пусть . Возьмем . Докажем, что .

Предположим, что , тогда существует , т.е. и . Тогда, . Получили противоречие. Следовательно, .

Следствие. Метризуемое пространство является - пространством.

Определение. Расстоянием от точки до множества в метрическом пространстве называется .