Дипломная работа: Многомерная геометрия

Определение 1: Скалярным произведением на векторном пространстве V называется операция, которая любой паре векторов a и b ставит в соответствие некоторое действительное число, обозначаем символом a b и обладающее следующими свойствами:11. Для любых векторов a , b V и любого вектора a b = b а ;12. Для любых двух векторов a , b V и любого числа .13. Для любых трёх векторов a, b, cV ;14. Для любого ненулевого вектора а V aa >0.

Определение 2: Векторное пространство V _n , в котором введена операция скалярного произведения векторов, удовлетворяющая аксиомам 11-14, называется евклидовым векторным пространством. Будем обозначать его символом Е _n .

На основе определения 1 можно ввести понятие длины вектора и величины угла между векторами.

Число аа называется скалярным квадратом вектора а и обозначается а ² . Из аксиомы 14 следует, что а ² >0, следовательно, - действительное положительное число. Оно называется длиной или нормой вектора и обозначается: . Если 1, то вектор а называется единичным.

На основе аксиом 11-14 можно указать следующие утверждения: Для любых векторов a, b ₁ , b ₂ ,…, b _n выполняется равенство

.

, где а – произвольный вектор;

Если , то , а если , то ;Если , то .

Можно показать, что если , то вектор 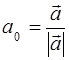является единичным, его называют ортом вектора а . Он определяет то же направление, что и вектор а .

При решении метрических задач, т. е. задач, связанных с измерением длин векторов и величин углов, пользуются ортонормированным базисом.

Определение : Базис называется ортонормированным, если все его векторы единичные и попарно ортогональны, т. е. если и () при .

Теорема . В евклидовом пространстве Е _n существуют ортонормированные базисы.

Действительно, если (а ₁ , а ₂ ,…, а _n ) – ортогональный базис, то можно рассмотреть векторы

, ,…, .

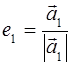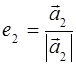Ясно, что базис (е ₁ , е ₂ ,…, е _n ) ортонормированный, так как его векторы единичные и попарно ортогональны.

Введём обозначения: В =(i , j ) или B=(i , j , k ) – ортонормированные базисы евклидовых векторных пространств Е ₂ и Е ₃ соответственно.

§ 4. Понятие точечно-векторного аффинного n-мерного пространства

В § 2 и § 3 были аксиоматически определены различные векторные пространства: линейные векторные, n-мерные векторные, евклидовы векторные. Но для построения геометрии, то есть для рассмотрения различных геометрических фигур, одних векторов недостаточно, нужны ещё точки.

Аксиоматизируя построение вектора по двум точкам, введём следующее определение.

Определение . Аффинным пространством называют некоторое множество А^* элементов произвольной природы, называемых точками, для которого задано

а) некоторое векторное пространство V;

б) отображение, которое любым двум точкам А и В А ^* ставит в соответствие некоторый вектор из V , обозначаемый АВ .

При этом требуется выполнение следующих аксиом:

15. Для любой точки А А ^* и любого вектора А из V существует единственная точка ВА^* и любого вектора аV существует единственная точка В А ^* , такая что АВ =а .

16. Для любых трёх точек А, В, С A ^* имеет место равенство АВ +ВС =АС .

Аксиома 15 называется аксиомой откладывания вектора от точки, а аксиома 16 – аксиомой треугольника, из которой следует правило треугольника и правило параллелограмма сложения векторов.

Размерность пространства V называется размерностью соответствующего аффинного пространства А ^* и обозначается символом А ^* _n .

Отметим некоторые важные следствия из аксиом 15-16.

При любом выборе точки А вектор АА нулевой.

Если АВ =0, то точки А и В совпадают.