Дипломная работа: Многомерная геометрия
Если АВ=С D , то АС=В D .
Для произвольных точек А 1 , А 2 ,…, А n выполняется равенство А 1 А 2 + А 2 А 3 + А n-1 А n = А 1 А n (правило многоугольника сложения векторов).
Пространство А* n содержит бесчисленное множество точек.На основе аксиом 1-10 и 15-16 аффинной геометрии нельзя ввести понятий длин отрезков и величин (мер) углов. Эти понятия можно ввести, используя скалярное произведение векторов.
Как известно, введение в V n скалярного произведения векторов приводит к евклидову векторному пространству Е n .
Определение . Аффинное пространство А n * , в котором соответствующее ему векторное пространство V n превращено в евклидово векторное пространство Е n , называется евклидовым n-мерным пространством.
Для этого пространства введём обозначение Е n . Согласно определению ясно, что всякое аффинное пространство А n * можно превратить в евклидово пространство Е n , задавая на векторном пространстве V n скалярное произведение векторов, удовлетворяющее аксиомам 11-14 (§ 3).
Таким образом, в Е n выполняются аксиомы 1-16.
На основе аксиом евклидова пространства строится евклидова геометрия.
В евклидовой геометрии, очевидно, справедлива вся изложенная выше теория аффинной геометрии. Но пространство Е n обладает метрическими свойствами, которые следуют из аксиом скалярного произведения векторов и связаны с измерением длин отрезков и мер углов. Поэтому евклидову геометрию называют ещё метрической геометрией.
Метрические аксиомы позволяют установить метрику евклидова пространства, т. е. расстояния между его точками. Определим сначала модуль |a| вектора а как неотрицательный корень из его квадрата, т. е.
(4.1)
Векторы, модуль которых равен 1, будем называть единичными векторами; единичный вектор 
будем обозначать а 0 .
Будем считать расстоянием между точками А и В модуль вектора АВ ; будем обозначать это расстоянием АВ .
Таким образом, расстояние АВ между точками А (х ) и В (y ) определяется соотношением
(4.2)
Из определения расстояния следует, что
Расстояние симметрично, т. е.
АВ =ВА (4.3)
Расстояние позитивно, т. е. (4.4) AB ≥ 0, причём знак равно имеет место только при совпадении точек А и В .Покажем, что для расстояний между точками евклидова пространства помимо свойств 1 и 2 выполняется также «неравенство треугольника».расстояние между всякими двумя точками не более суммы расстояний между этими точками и третьей точкой, т. е.
АС ≤ АВ + ВС (4.5)
Множество точек, для всяких двух точек А и В которого определено число АВ, удовлетворяющего условиям 1-3, называется метрическим пространством. Для доказательства неравенства треугольника докажем так называемое неравенство Коши
(4.6)
Скалярный квадрат вектора a – tb неотрицателен при любом вещественном t
, т. е. 
.
В случае b = 0 обе части неравенства (4.6) равны 0, т. е. неравенство выполняется автоматически.
Если 
, получим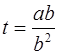 
.
Тогда неравенство примет вид
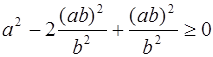, т. е. 
,
что равносильно неравенству (4.6). Рассмотрим три точки А (х ), В (у ) и С (z ). Тогда 