Дипломная работа: Моделі відкритої мережі

б) Якщо на приладі немає заявок, те вступник позитивна заявка починає обслуговуватися;

в) Якщо на приладі заявка позитивна, те негативна заявка, що прийшла, вибиває заявку із приладу й позитивна заявка губиться.

г) Якщо в черзі заявок позитивних, те прихожа негативна заявка, витісняє останню (позитивну) заявку й у черзі стає заявка ( -ая позитивна й негативна заявка губиться).

Стан мережі описується випадковим процесом

,

де – число позитивних заявок у момент , відповідно в першому, другому, третьому вузлі. Відповідно до розділу 1 і з огляду на формулу (3.1) – марковський процес.

Таким чином, відповідно до визначення 1.3 і вищесказаному, побудована марковська модель відкритої мережі із трьома вузлами й різнотипними заявками.

3.1 Складання рівнянь трафіка

Розглянемо ізольований -й вузол ( ), уважаючи, що на нього надходить потік заявок інтенсивності . Граф переходів зобразиться в такий спосіб.

Тоді відповідно до малюнка 3.1.1, одержимо наступні співвідношення

, , (3.1.1)

де .

Відповідно до малюнка 3.1

, . (3.1.2)

Для марковської моделі мережі із трьома вузлами й різнотипними заявками рівняння трафіка мають такий вигляд:

,

,

,

,

,

.

З огляду на формулу (3.1.2) запишемо ще три рівняння

,

,

.

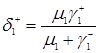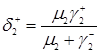Таким чином, рівняння трафіка мають такий вигляд

. (3.1.3)

, (3.1.4)

, (3.1.5)