Дипломная работа: Моделирование динамических процессов в пневмоцилиндре

Т_М - температура воздуха в магистрали.

Из решения (1.5) совместно с уравнением (1.7) и определяют давление Р₁ в полости как функцию времени. Из формулы (1.7) следует, что расход G_M является функцией отношения давлений σ, в числителе которого всегда находится давление той среды, куда истекает газ, а в знаменателе - давление среды, откуда вытекает этот газ.

Представим формулу (1.7) расхода воздуха из магистрали σ_М в более удобном виде:

, (1.7)

где ;

;

.

При Т м = 293 К расход G_M = 0,00912, причем Рм в Па. Чтобы найти максимум расходной функции ер (а), приравняем нулю ее производную , откуда получим, критическое отношение давлений

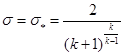= 0,5282 (при к = 1,4). (1.9)

Подставим в уравнение (1.6) значение расхода G_M из выражения (1.8), получим уравнение для определения давления в полости наполнения в общем виде:

(1.10)

Объем V₁ рабочей полости равен произведению площади поршня F₁ на перемещение поршня х (с учетом его начальной координаты х₀₁ ), т.е. . Подставим это значение в (1.10), получим

, (1.11)

где ,

V ₀₁ - начальный объем рабочей плости,

F₁ – площадь поршня.

Если это уравнение выразить относительно _1, то после интегрирования найдем время наполнения постоянного объема от начального безразмерного давления σ₁₁ до заданного давления σ₁₂ :

(1.12)

Значения функций Ψ₁ (σ₁₁ ) и Ψ₁ (σ₁₂ ) определяем по графику, приведенному на рис.3.

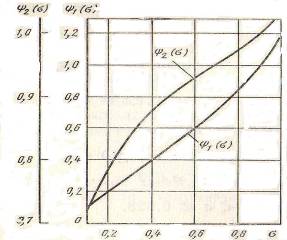
Рисунок 3

Формулу (1.13) применяют для определения времени наполнения полости постоянного объема до заданного давления, в том числе и для определения времени ₃ (см. циклограмму на рис. 3).

1.3 Процесс истечения сжатого воздуха из выхлопной полости привода

При перемещении поршня 1 (см. рис. 1) в дифференциальном приводе давление сжатого воздуха в выхлопной полости 2 может повышаться вследствие уменьшения ее объема. В этом случае происходит истечение воздуха в магистраль.

Здесь также может быть применен первый закон термодинамики (1.1), но в этом уравнении следует поставить знак минус в левой части, так как происходит истечение воздуха

-dQ2 = dU2 + dL2.(1.14)

Соответственно изменяем индекс 1, относящийся к рабочей полости, на индекс 2 выхлопной полости. Далее, выкладки будут аналогичны приведенным в формулах (1.1) - (1.5). Остановимся на последнем выражении

-k∙R∙Т₂ dm₂ = V₂ dР₂ + k∙Р₂ dV₂ . (1.15)

Имея в виду, что