Дипломная работа: Моделирование динамических процессов в пневмоцилиндре

получаем ₂ dР₂ + k∙Р₂ d₂ = 0 или после интегрирования и потенцирования этого выражения - P₂ ∙ = const - уравнение адиабаты.

Расход воздуха из ограниченного объема V₂ в магистраль описывается также формулой Сен-Венана и Ванцеля, однако в ней следует положить Т_М = Т₂ , Рм =Р₂ имея при этом в виду, что все эти величины являются переменными:

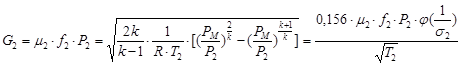, (1.16)

где 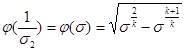при 0,528 < σ < 1.

Подставив в уравнении (1.15) dm₂ = ₂ dt и ₂ из (1.16), получим уравнение для определения давления в выхлопной полости, соединенной с магистралью:

, (1.17)

где - площадь поршня со стороны штоковой полости.

Температура Т₂ в уравнении (1.17) может быть выражена через давление Р₂ на основании уравнения адиабаты:

.(1.18)

Тогда получим следующее уравнение для определения давления воздуха при истечении его из ограниченного объема:

(1.19)

При обратном ходе подготовительное время t₃ ^’ будет характеризовать время истечения полости до необходимого давления, определяемого нагрузкой.

Однако при обратном ходе эта полость становится выхлопной, соединенной с атмосферой. Давление будет изменяться по уравнению (1.19), в котором следует вместо 1/σ₂ подставить σа/σ₂ так как истечение будет происходить в атмосферу пропорционально отношению давлений Ра/Р₂ = σа/σ₂ где σа = Ра/Р_м , σ₂ = Р₂ /Р_М .

Так как при обратном ходе поршневая полость становится выхлопной, присвоим ей индекс 2:

,(1.20)

где при 0 < σ < 0,528;

при 0,528 < σ < 1.

Расход воздуха при истечении из ограниченного объема полости в атмосферу определяем по формуле (1.16), в которой принимаем Р_М = Ра:

, (1.21)

где .

При Т_м = 293 К расход ₂ = 0,00912.

Для определения подготовительного и заключительного времени в уравнение (1.20) следует подставить х = 0, dx = 0. Если полученное уравнение выразить относительно t, то получим после интегрирования время истечения воздуха из постоянного объема в диапазоне изменений давлений σ₂₁ (Р₂₁ ) до σ₂₂ (Р₂₂ ):

. (1.22)

Значения Ψ₂ () и Ψ₂ (), определяем по графику на рис.3, стр. 11.

1.4 Динамический расчет дифференциального привода

Уравнение движения поршня дифференциального привода имеет вид:

Р, (1.23)

где - масса поршня;