Дипломная работа: Некоторые задачи оптимизации в экономике
Изучение экономических приложений математических дисциплин, составляющих основу актуальной экономической математики, позволяет приобрести некоторые навыки решения экономических задач и расширить знания в этой области.
Целью данной работы является изучение некоторых оптимизационных методов, применяемых при решении экономической задач.
При написании дипломной работы были поставлены следующие задачи:
· Рассмотрение некоторых экономических задач и составление математических моделей.
· Изучение некоторых математических методов, применяемых для решения оптимизационных задач в экономике.
· Практическое решение задач.
1. Математические модели в экономике
Современная экономическая теория включает как естественный, необходимый элемент математические модели и методы. Использование математики в экономике позволяет, во-первых, выделить и формально описать наиболее важные, существенные связи. Во-вторых, из чётко сформулированных исходных данных и соотношений можно сделать выводы, адекватные изучаемому объекту в той же мере, что и сделанные предпосылки. В-третьих, методы математики позволяют индуктивным путем получать новые знания об объекте: оценить форму и параметры зависимостей его переменных, в наибольшей степени соответствующие имеющимся наблюдениям. В-четвертых, использование языка математики позволяет точно и компактно излагать положения экономической теории, формулировать её понятия.
Математические модели использовались с иллюстративными исследованиями ещё Ф. Кене (1758г., «Экономическая таблица»), А. Смитом (Классическая макроэкономическая модель), Д. Риккардо (Модель международной торговли). В XIX веке большой вклад в моделирование рыночной экономики внесли математики Л. Вальрас, О. Курно, В. Парето и другие. В XX веке математические методы моделирования применялись очень широко, с их использованием связаны практически все работы, удостоенные Нобелевской премии по экономике (Р. Солоу, В. Леонтьев, Л. Канторович и другие). Развитие макроэкономики, микроэкономики, прикладных дисциплин связано со все более высоким уровнем их формализации. Основу для этого заложил прогресс в области прикладной математики. В России в начале XX века большой вклад в математическое моделирование экономики внесли В.К. Дмитриев и Е.Е. Слуцкий. В 1960-е – 80-е годы экономико-математическое направление было связано, в основном, с попытками формально описать «систему оптимального функционирования социалистической экономики» (Н.П. Федоренко, С.С. Шаталин). Строились многоуровневые системы моделей народно – хозяйственного планирования, оптимизационные модели областей и предприятий.
Математическая модель экономического объекта – это его гомоморфное отображение в виде совокупности уравнений, неравенств, логических отношений, графиков. Иными словами, модель – это условный образ объекта, построенный для упрощения его исследования. Предполагается, что изучение модели дает новые решения в той или иной ситуации.
Можно выделить 3 этапа проведения математического моделирования в экономике:
1. ставятся цели и задачи исследования, проводится качественное описание объекта в виде экономической модели.
2. формируется математическая модель изучаемого объекта, осуществляется выбор методов исследования. Далее исследуется модель с помощью этих методов.
3. осуществляется обработка и анализ полученных результатов.
Математические модели, используемые в экономике, можно подразделить на классы по ряду признаков, относящихся к особенностям моделируемого объекта, цели моделирования и используемого инструментария: модели макро- и микроэкономические, теоретические и прикладные, оптимизационные и равновесные, статические и динамические.
Мы будем рассматривать некоторые оптимизационные модели. К оптимизационным моделям относят следующие: модель линейного программирования, нелинейного, динамического, сетевые модели. Будем рассматривать модели линейного и нелинейного программирования.
2. Некоторые понятия функций нескольких переменных
Многим экономическим явлениям присуща многофакторная зависимость, поэтому при изучении процессов в экономике вводят функции нескольких переменных.
Переменная y называется функцией нескольких переменных x 1 , x 2 ,…, xn , если существует отображение f : Rn → R . Множество всех точек М, участвующих в этом отображении, называется областью определения функции , где М(x 1 , x 2 ,…, xn ).
Наиболее часто встречается функция двух переменных. В экономике для её изучения широко применяются линии уровня.
Линиями уровня функции двух переменных y = f ( x 1 , x 2 ) называется проекция пересечения графика функции y = f ( x 1 , x 2 ) с горизонтальной плоскостью на плоскость Ох1 х2 , причём линия пересечения находится от плоскости Ох1 х2 на высоте С. Уравнение линии уровня имеет вид f ( x 1 , x 2 )=С. Число С в этом случае называется уровнем .
Как и в случае одной переменной, функция y = f ( x 1 , x 2 ) имеет узловые, определяющие структуру графика, точки. В первую очередь это точки экстремума. Точки экстремума функции двух переменных определяются аналогично точкам экстремума функции одной переменной
Сформулируем необходимое условие экстремума – многомерный аналог теоремы Ферма: Пусть точка ( ![]() ) - есть точка экстремума дифференцируемой функции y = f ( x 1 , x 2 ). Тогда частные производные
) - есть точка экстремума дифференцируемой функции y = f ( x 1 , x 2 ). Тогда частные производные![]() (
( ![]() ),
), ![]() (
( ![]() ) в этой точке равны нулю.
) в этой точке равны нулю.
Точки, в которых выполнены необходимые условия экстремума функции y = f ( x 1 , x 2 ) , т. е частные производные ![]() равны нулю, называются стационарными.
равны нулю, называются стационарными.
Равенство нулю частных производных выражает лишь необходимое условие, но недостаточное условие экстремума функции нескольких переменных.
|
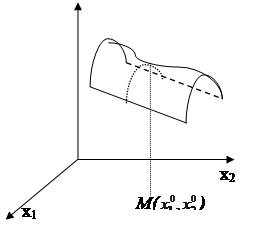
Достаточное условие экстремума функции двух переменных . Пусть функция y = f ( x 1 , x 2 ) :
a) определена в некоторой окрестности стационарной точки ( ![]() ) , в которой
) , в которой![]() (
( ![]() ) =0 и
) =0 и ![]() (
( ![]() )= 0;
)= 0;
b) имеет в этой точке непрерывные частные производные второго поряка![]() (
( ![]() ) =А,
) =А, ![]() (
( ![]() ) =
) = ![]() (
( ![]() ) =В,
) =В, ![]() (
( ![]() ) =С.
) =С.
Тогда, если ![]() =АС-В2 >0 , то в точке (
=АС-В2 >0 , то в точке ( ![]() ) функция имеет экстремум, причём, если А>0 минимум, А<0 – максимум. В случае
) функция имеет экстремум, причём, если А>0 минимум, А<0 – максимум. В случае ![]() =АС-В2 <0 , функция y = f ( x 1 , x 2 ) экстремума не имеет. Если
=АС-В2 <0 , функция y = f ( x 1 , x 2 ) экстремума не имеет. Если ![]() =АС-В2 =0 , то вопрос о наличии экстремума остаётся открытым. Требуются другие методы определения экстремума. [11]
=АС-В2 =0 , то вопрос о наличии экстремума остаётся открытым. Требуются другие методы определения экстремума. [11]
В экономических задачах чаще встречаются задачи на условный экстремум. Перейдем к рассмотрению таких задач.
3. Задача математического программирования (ЗМП).
1) Общая постановка задачи