Дипломная работа: Некоторые задачи оптимизации в экономике
Стандартную задачу можно привести к каноническому виду, путём введения дополнительных неотрицательных переменных. Т.е. свести к системе m линейных уравнений с n переменными.
Любые m переменных системы m линейных уравнений с n переменными (m<n) называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными или (свободными).
Базисным решением системы m линейных уравнений с n переменными называют решение, в котором все m-n неосновных переменных равны нулю.
Для обоснования свойств ЗЛП и методов её решения, рассмотрим 2 вида записи канонической задачи.
1 вид – матричная форма записи: С=(c1 ,c2 …cn ,c0 ).
Х=![]() А=
А=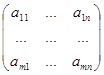 В=
В=![]() (3.3)
(3.3)
F = CX → min ( max )
AX = B , X ≥0
2 вид – векторная форма записи:
F = CX → min ( max )
р1 x 1 +р2 x 2 +…+р n xn =р. Х≥0 .
р1 =![]() р2 =
р2 =![]() … рn =
… рn =![]() .
.
Для того чтобы рассмотреть теоретические основы метода линейного программирования, определим понятие выпуклого множества точек, дав ему определение в аналитической форме:
Множество точек является выпуклым, если оно вместе с любыми своими двумя точками содержит их произвольную линейную комбинацию. Точка Х является выпуклой линейной комбинацией точек Х1 , Х2 , … Х n ,если выполняются условия Х= α 1 x 1 + α 2 x 2 +…+ αn xn , αj ≥0, ( j =1,…, n ) , ![]() .
.
Теорема 1 . Выпуклый линейный многогранник является выпуклой линейной комбинацией своих угловых точек. (Примем без доказательства).
Теорема 2 . Множество всех допустимых решений системы ограничений ЗЛП является выпуклым .
□ Пусть Х1 =( x![]() , x
, x![]() , …,х
, …,х ![]() ) и Х2 =( x
) и Х2 =( x![]() , x
, x![]() , …,х
, …,х ![]() ) - два допустимых решения задачи (3.3), заданной в матричной форме. Тогда АХ1 =В и АХ2 =В . рассмотрим выпуклую линейную комбинацию решений Х1 и Х2 , т.е. Х= α 1 Х1 + α 2 Х2 при α 1 ≥0, α 2 ≥0 и α 1 + α 2 =1 . Покажем, что она также является допустимым решением системы АХ=В . В самом деле, АХ=А( α 1 Х1 + α 2 Х2 ) =α 1 АХ1 +(1- α 1 )АХ2 = α 1 В+(1- α 1 )В=В , т.е. решение удовлетворяет системе ограничений. Но т.к. Х1 ≥0, Х2 ≥0, α 1 ≥0, α 2 ≥0 , то и Х ≥0 , т.е. решение Х удовлетворяет условию (3.3). ■
) - два допустимых решения задачи (3.3), заданной в матричной форме. Тогда АХ1 =В и АХ2 =В . рассмотрим выпуклую линейную комбинацию решений Х1 и Х2 , т.е. Х= α 1 Х1 + α 2 Х2 при α 1 ≥0, α 2 ≥0 и α 1 + α 2 =1 . Покажем, что она также является допустимым решением системы АХ=В . В самом деле, АХ=А( α 1 Х1 + α 2 Х2 ) =α 1 АХ1 +(1- α 1 )АХ2 = α 1 В+(1- α 1 )В=В , т.е. решение удовлетворяет системе ограничений. Но т.к. Х1 ≥0, Х2 ≥0, α 1 ≥0, α 2 ≥0 , то и Х ≥0 , т.е. решение Х удовлетворяет условию (3.3). ■
Итак, доказано, что множество всех допустимых решений ЗЛП является выпуклым, которое будем называть многогранником решений .
Ответ на вопрос, в какой точке многогранника решений возможно оптимальное решение ЗЛП, даёт следующая теорема.
Теорема 3. Если ЗЛП имеет оптимальное решение, то линейная функция F принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в произвольной точке, являющейся выпуклой линейной комбинацией этих точек .
 □ Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х1 ,Х2, …,Х n , аоптимальное решение через Х* . Тогда F (Х* ) ≥ F ( X ) , для всех точек многогранника решений. Если Х* угловая, то первая часть теоремы доказана. Предположим, что Х* не является угловой точкой, тогда Х* , на основании теоремы 1, можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х* = α 1 x 1 + α 2 x 2 +…+ α р x р , αj ≥0, ( j =1,…, n ),
□ Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х1 ,Х2, …,Х n , аоптимальное решение через Х* . Тогда F (Х* ) ≥ F ( X ) , для всех точек многогранника решений. Если Х* угловая, то первая часть теоремы доказана. Предположим, что Х* не является угловой точкой, тогда Х* , на основании теоремы 1, можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х* = α 1 x 1 + α 2 x 2 +…+ α р x р , αj ≥0, ( j =1,…, n ), ![]() . Т.к.
. Т.к.
F (Х* )= F ( α 1 x 1 + α 2 x 2 +…+ α р x р )= α 1 F ( x 1 )+ α 2 F ( x 2 )+…+ α р F ( x р ) . (3.4)
В этом выражении среди значений F ( Xj )( j =1,2,…, p ) выберем максимальное. Обозначим его через М , т.е. М= max F ( Xj ) . Тогда
α 1 F ( x 1 )+ α 2 F ( x 2 ) +…+ α р F ( x р )≤ α 1 М+ α 2 М +…+ α р М = М( α 1 + α 2 +…+ α р ) =М .
Значит F (Х* )≤М . Пусть М= F ( Xk ) , т.е. соответствует угловой точке Xk (1≤к≤р) .
Тогда F (Х* ) ≤ F ( Xk ) . Но по предположению Х* - оптимальное решение, поэтому F (Х* )≥ F ( Xk )=М , следовательно, F (Х* )=М= F ( Xk ) , где Xk - угловая точка. Итак, существует угловая точка Xk , в которой линейная функция принимает максимальное значение.
Для доказательства второй части теоремы допустим, что F (Х) принимает максимальное значение более чем в одной угловой точке, например в точках Х1 , Х2 , … Х q , где 1≤ q ≤ р ; тогда F (Х1 )= F (Х2 )=…= F (Х n )= M .
Пусть Х выпуклая линейная комбинация этих угловых точек, т.е. Х= α 1 Х1 + α 2 Х2 + …+ αq Х q , αj ≥0, ( j =1,…, q ), ![]() . В этом случае, учитывая, что функция F (Х) – линейная, получим F (Х)= F ( α 1 Х1 + α 2 Х2 +…+ αq Х q )= α 1 F (Х1 )+ + α 2 F (Х2 )+…+ αq F (Х q )= α 1 M + α 2 M +…+ αq M = M
. В этом случае, учитывая, что функция F (Х) – линейная, получим F (Х)= F ( α 1 Х1 + α 2 Х2 +…+ αq Х q )= α 1 F (Х1 )+ + α 2 F (Х2 )+…+ αq F (Х q )= α 1 M + α 2 M +…+ αq M = M![]() = M , т.е. линейная функция F принимает максимальное значение в произвольной точке Х , являющейся выпуклой линейной комбинацией угловых точек Х1 , Х2 , … Х q ■
= M , т.е. линейная функция F принимает максимальное значение в произвольной точке Х , являющейся выпуклой линейной комбинацией угловых точек Х1 , Х2 , … Х q ■
Замечание. Требование ограниченности многогранника решений в теореме является существенным, т.к. в случае неограниченной многогранной области не каждую точку можно представить выпуклой линейной комбинацией её угловых точек.
Доказанная теорема является фундаментальной, т.к. она указывает принципиальный путь решения ЗЛП.
Рассмотрим геометрический метод решения ЗЛП в случае функции двух переменных.
Было доказано, что оптимальное решение ЗЛП находится, по крайней мере, в одной из угловых точек многогранника решений.
Рассмотрим задачу в стандартной форме с двумя переменными.
F=c1 x1 +c2 x2 + с 0 →min(max) ,
![]() При ограничениях а11 х1 + а12 х2 ≤ b 1 ,
При ограничениях а11 х1 + а12 х2 ≤ b 1 ,
а21 х1 + а22 х2 ≤ b 2 ,