Дипломная работа: Обобщ нно булевы решетки
Если ![]() и
и ![]() , то говорят, что
, то говорят, что ![]() меньше
меньше ![]() или
или ![]() больше
больше ![]() , и пишут
, и пишут ![]() или
или ![]() .
.
Примеры упорядоченных множеств:
1. Множество целых положительных чисел, а ![]() означает, что
означает, что ![]() делит
делит ![]() .
.
2. Множество всех действительных функций ![]() на отрезке
на отрезке ![]() и
и ![]() означает, что
означает, что ![]() для
для ![]() .
.
Цепью называется упорядоченное множество, на котором для любых ![]() имеет место
имеет место ![]() или
или ![]() .
.
Используя отношение порядка, можно получить графическое представление любого конечного упорядоченного множества P . Изобразим каждый элемент множества P в виде небольшого кружка, располагая x выше y , если ![]() . Соединим x и y отрезком. Полученная фигура называется диаграммой упорядоченного множества P .
. Соединим x и y отрезком. Полученная фигура называется диаграммой упорядоченного множества P .
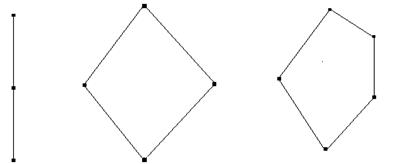 |
??????? ???????? ?????????????? ?????????:
1.2. Решётки
Верхней гранью подмножества Х в упорядоченном множестве Р называется элемент a из Р , больший или равный всех x из X .
Точная верхняя грань подмножества X упорядоченного множества P – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом sup X и читается «супремум X ».
Согласно аксиоме антисимметричности упорядоченного множества, если точная верхняя грань существует, то она единственна.
Понятия нижней грани и точной нижней грани (которая обозначается inf X и читается «инфинум ») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань X существует, то она единственна.
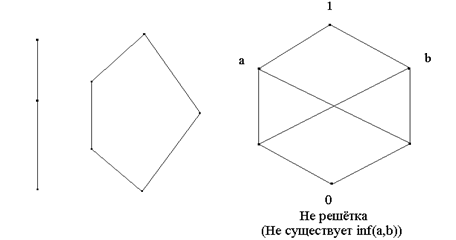 |
Решёткой
Примеры решёток:
Примечание. Любая цепь является решёткой, т.к. ![]() совпадает с меньшим, а
совпадает с меньшим, а ![]() с большим из элементов
с большим из элементов ![]() .
.
Наибольший элемент, то есть элемент, больший или равный каждого элемента упорядоченного множества, обозначают 1, а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают 0.
На решётке можно рассматривать две бинарные операции:
![]() - сложение и
- сложение и
![]() - произведение
- произведение
Эти операции обладают следующими свойствами:
1. ![]() ,
, ![]() идемпотентность;
идемпотентность;
2. ![]() ,
, ![]() коммутативность;
коммутативность;
3. ![]() ,
, ![]() ассоциативность;
ассоциативность;
4. ![]() ,
, ![]() законы поглощения.
законы поглощения.
ТЕОРЕМА 1.1. Пусть L - множество с двумя бинарными операциями ![]() , обладающими свойствами (1) – (4). Тогда отношение
, обладающими свойствами (1) – (4). Тогда отношение ![]() (или
(или ![]() ) является порядком на L , а возникающее упорядоченное множество оказывается решёткой, причём:
) является порядком на L , а возникающее упорядоченное множество оказывается решёткой, причём: ![]() и
и ![]() .
.
Доказательство. Рефлексивность отношения ![]() вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
![]()
![]()
Если ![]() и
и ![]() , то есть
, то есть ![]() и
и ![]() , то в силу свойства (2), получим
, то в силу свойства (2), получим ![]() . Это означает, что отношение
. Это означает, что отношение ![]() антисимметрично.
антисимметрично.
Если ![]() и
и ![]() , то применяя свойство (3), получим:
, то применяя свойство (3), получим: ![]() , что доказывает транзитивность отношения
, что доказывает транзитивность отношения ![]() .
.
Применяя свойства (3), (1), (2), получим:
![]() ,
,
![]() .
.
Следовательно, ![]() и
и ![]() .
.
Если ![]() и
и ![]() , то используя свойства (1) – (3), имеем:
, то используя свойства (1) – (3), имеем:
![]() , т.е.
, т.е. ![]() .
.