Дипломная работа: Положительные и ограниченные полукольца 2

. Очевидно.

. По свойству 2 следует , тогда:

и .

Эти условия наряду с ассоциативностью, коммутативностью и идемпотентными законами определяют дистрибутивную решетку.

V . В ограниченном полукольце единица 1 – единственный обратимый элемент.

Доказательство.

Пусть есть некоторый обратимый элемент u ,

и

VI . Пусть a – фиксированный элемент полукольца S , тогда каждое из утверждений влечет следующее утверждение:

1. a +1=1 ;

2.

3.

Доказательство.

. Докажем методом математической индукции по числу n .

I. База. к=1 . (выполняется по условию).

II. Индуктивное предположение. Пусть для к< n условие выполняется, т.е.

Рассмотрим для k=n

и a +1=1

Из Iи IIСледует .

. .

Можно выбрать из всего количества N , некоторое число, для которого тоже данное выражение будет верно.

Примером того , что условие 3 не влечет условие 1 является полукольцо матриц . Зафиксируем элемент , где . Для n =2

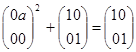верно, но совсем неверно.

VII . Если S – полукольцо с мультипликативным сокращением и аддитивно идемпотентно, то все утверждения предыдущего свойства равносильны.

Доказательство.

Осталось доказать .

Имеем . Добавим к правой и левой части выражения равные элементы :

В силу аддитивной идемпотентности мы можем подбирать коэффициенты перед . В соответствии с биномом Ньютона, подберем коэффициенты и получим:

Используя мультипликативную сократимость, получим a +1=1 . Что и доказывает равносильность условий 1 – 3.

VIII . Пусть S – ограниченное полукольцо, и существует такое , что для всех . Тогда:

1. для всех ;

2. - коммутативное ограниченное полукольцо с 1, где I – множество всех мультипликативных идемпотентов из S , а операцияопределяется так:

.