Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа
Определение: Алгебра <P, +, ×> называется полуполем , если
(1) <Р, +> – коммутативная полугруппа с 0;
(2) <Р, ×> – группа с 1;
(3) Дистрибутивность
a. ![]()
b. ![]()
(4) ![]()
Не сложно показать, что Q + является полуполем.
Определение: Пусть Р – подполуполе полуполя F , ![]() , тогда простым расширением полуполя P с помощью элемента a называется наименьшее подполуполе полуполя F , содержащее множество P и элемент a . Простое расширение P с помощью a обозначается P (a ).
, тогда простым расширением полуполя P с помощью элемента a называется наименьшее подполуполе полуполя F , содержащее множество P и элемент a . Простое расширение P с помощью a обозначается P (a ).
1.2. Простое расширение Q + (a )
Теорема 1.2.1. Произвольное полутело либо аддитивно идемпотентно, либо содержит копию Q + в качестве полутела.
Доказательство. Предположим, что S – неидемпотентное полутело, т.е. найдется такой ненулевой элемент s ÎS , что s +s ¹s . Откуда
![]() .
.
Рассмотрим суммы единиц. Через ![]() обозначим сумму k единиц (при k ÎN ). Так как любое полутело является антикольцом, то
обозначим сумму k единиц (при k ÎN ). Так как любое полутело является антикольцом, то ![]() . Покажем, что суммы различного числа единиц в S различны. Допустим от противного, что
. Покажем, что суммы различного числа единиц в S различны. Допустим от противного, что ![]() при некоторых натуральных m <n . Положим l = n - m ÎN . Тогда
при некоторых натуральных m <n . Положим l = n - m ÎN . Тогда ![]() . Прибавляя к обеим частям этого равенства элемент
. Прибавляя к обеим частям этого равенства элемент ![]() , получим
, получим
![]() .
.
Применяя эту процедуру несколько раз, будем иметь
![]() для любого t ÎN .
для любого t ÎN .
По свойству Архимеда, найдется такое t ÎN , что tl >n. При k= tl имеем ![]() и n< k . Тогда
и n< k . Тогда
![]() .
.
Откуда 1=1+1 (![]() ). Получили противоречие.
). Получили противоречие.
Следовательно, полутело S содержит аддитивную копию N . Но тогда S содержит и частные сумм 1, т.е. содержит копию полуполя Q + , причем, очевидно, операции в Q + и S согласованы.
■
Теорема 1.2.2. 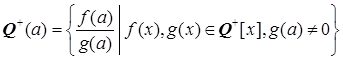 - простое расширение полуполя Q + .
- простое расширение полуполя Q + .
Доказательство. Заметим, что Q + (a ) – полуполе. Кроме того, а Î Q + (a ). Это не сложно увидеть, взяв ![]() . Очевидно
. Очевидно ![]() .
.
Предположим, что есть полуполе P меньшееQ + (a ), содержащее а и Q + . Тогда оно содержит все выражения вида ![]() . Так как P – полуполе, то
. Так как P – полуполе, то 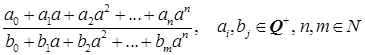 . Таким образом,
. Таким образом, ![]() . Так как P – минимальное полуполе, то
. Так как P – минимальное полуполе, то ![]() . То есть,
. То есть, ![]() –простое расширение полуполя Q + .
–простое расширение полуполя Q + .
■
Аналогично доказывается следующее утверждение.
Теорема 1.2.3.  - простое расширение поля Q .
- простое расширение поля Q .
1.3. Минимальное соотношение алгебраического элемента над полуполем рациональных неотрицательных чисел
Пусть а – алгебраическое число. Тогда минимальный многочлен F числа а имеет степень ≥ 1. Тогда обозначим через f многочлен, составленный из положительных одночленов многочлена F , а многочлен g составим из отрицательных членов, взятых с противоположными знаками. Тогда ![]() .
. ![]() , тогда
, тогда ![]() .
.
Покажем, что любое равенство ![]() получается из
получается из ![]() , где
, где ![]() . Заметим, что
. Заметим, что ![]() , так как а – корень
, так как а – корень ![]() , а
, а ![]() – минимальный многочлен для a . Представим
– минимальный многочлен для a . Представим ![]() , где
, где ![]() составлен из положительных одночленов многочлена h , а
составлен из положительных одночленов многочлена h , а ![]() ‑ составлен из отрицательных одночленов многочлена h , взятых с противоположным знаком. Таким образом,
‑ составлен из отрицательных одночленов многочлена h , взятых с противоположным знаком. Таким образом,
![]()
Приведем подобные члены в паре ![]() , и найдем такой
, и найдем такой ![]() , что
, что
![]() ,
, ![]()
не имеют подобных членов.
Аналогично найдем ![]() , что
, что
![]() и
и
![]()
не имеют подобных членов.
Получаем
![]()
Так как ![]() не имеют подобных членов и
не имеют подобных членов и ![]() не имеют подобных членов, то
не имеют подобных членов, то
![]() ,
, ![]() или
или
![]() ,
, ![]() .
.